前缀和和差分基础浅析

前缀和

定义：使用s[N]表示数组q[N]的前缀和数组，s[i]表示q[1-i]的元素的和
公式：
注意，下标范围为1-N，且s[0]=0

差分

定义：前缀和的逆运算，假想一个d[N]，使得q[N]是d的前缀和数组，那么d[N]就称为q的差分。
公式：
注意，d下标范围为1-N

前缀和和差分的应用

求一段数的和O(1)

只需要事先处理得到q数组的前缀和s数组，就可以通过在O(1)时间内完成一段数的求和

对一段数加上某个数O(1)

假设我们已经有了差分数组，我们只需要对其求一遍前缀和即可得到原数组，时间复杂度为O(n)
我们对d[i]加上c后，a[i]~最后都会加上c（根据前缀和的定义），所有如果想要给一段数(l,r)都加上c，就只需要d[l]+c，d[r+1]-c

对子矩阵求和O(1)

对一维进行扩展可以得到二维区间和=，图像直观解释如下图：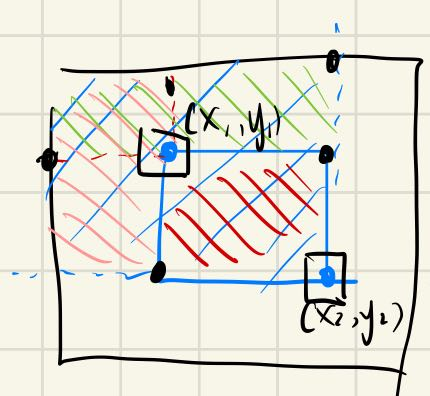

对二维区间加上某个数O(1)

画图可以清楚的解释该算法：

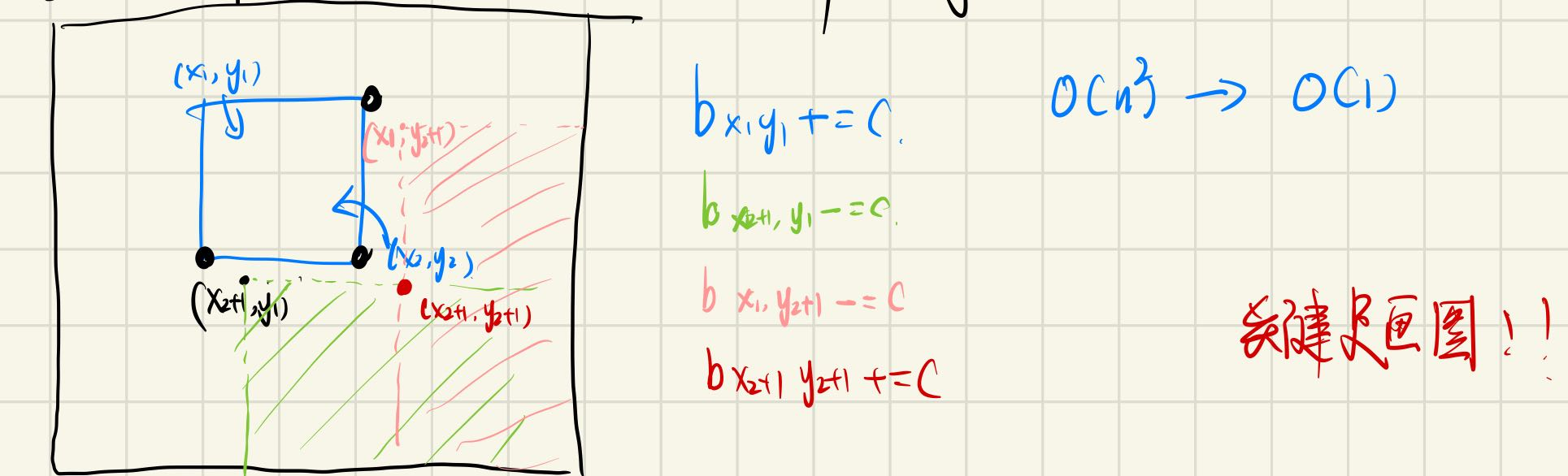
代码如下：

template<int n,int m>
void diffAdd2D(int (&diff) [n][m], int x1,int y1,int x2,int y2,int c){
    diff[x1][y1]+=c;
    diff[x1][y2+1]-=c;
    diff[x2+1][y1]-=c;
    diff[x2+1][y2+1]+=c;
}

注：在代码里我使用了二维数组传参的一种优美方法（使用模板推导出二维数组维度），在函数调用时无须指明维度大小，在函数体内也可以直接索引，从而可以减少代码量。

同理可以进行推广到三维甚至多维数组，代码如下：

template<int n, int m, int q>
void test3Dimens(int (&test)[n][m][q], int x1,int y1,int z1,int c){
    test[x1][y1][z1]-=c;
}

const int Q = 110;
int test3D[Q][Q][Q];

int multiDimenTest(){
    test3D[1][2][3]=6;
    test3Dimens(test3D,1,2,3,6);
    cout<<test3D[1][2][3];
    return 0;
}

推广：3D空间求和O(1)

应该不会考类似的题，但是对于拓展思维应该还是有用的

template<int n, int m, int q>
void 3D_Sum(int (&test)[n][m][q], int x1,int y1,int z1,int x2,int y2,int z2){
    return test[x2][y2][z2]-test[x2][y1-1][z2]-test[x1-1][y2][z2]-test[x2][y2][z1-1]+test[x2][y1-1][z1-1]+test[x1-1][y2][z1-1]+test[x1-1][y1-1][z2]-test[x1-1][y1-1][z1-1];
}