数论

质数

质数和和数是针对严格大于1的整数定义的，如果只包含1和本身两个约数，就被称为质数，否则为和数。

质数的判定

试除法 O(n)

bool is_prime(int n){
    if(n<2) return false;
    for(int i=2;i<n;i++)
        if(n%i==0) return false;
    return true;
}

我们可以发现n的所有约数都是成对出现的，即若d为n的约束，那么n/d也为n的约数。所以我们不需要枚举所有数，只需要枚举的数即可，也就是说d只需枚举到即可

优化 O()

不推荐使用sqrt(n)这个函数，也不推荐i*i<=n的写法，因为可能存在溢出风险，所以推荐写法为：i<=n/i

分解质因数

试除法 O(n)

从小到大尝试n的所有因数，因为每次都会把因子除干净，所以不用担心满足n%i==0的数i会是和数。

void divide(int n){
    for(int i=2;i<n;i++){
        if(n%i==0){ // i 一定是质数
            int cnt = 0;
            while(n%i==0){
                n/=i;
                cnt++;
            }
            printf("%d %d",i,cnt);
        }
    }
}

优化最坏O()

hints: n中最多只包含一个大于sqrt(n)的质因子，所以可以枚举所有小于sqrt的质因子，如果最后剩下的因子n，若大于1直接输出即可。

求从1~n的所有质数

筛法 O(nlogn)

bool st[N]; //为false代表没有被筛掉
int prime[N];
void get_prime(int n){
    int cnt = 0;
     for(int i=2;i<=n;i++){
         if(!st[i]){
             prime[cnt++]=i;
         }
         for(int j=i+i;j<=n;j+=i) st[j] = true;
     }
}

优化：埃氏筛法 O(nloglogn)

根据基本分解定理，每个数只需要被素数筛掉就可以了，所有可以把第二个循环放到if里。

线性筛法

void get_primes(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0;primes[j] <= n/i ; j++){
            st[primes[j]*i] = true;
            if(i%primes[j] == 0) break;
        }
    }
}

正确性证明：

论断：如果是和数，只会被最小质因子筛掉，且一定能被筛掉

从小到大枚举所有质数，每一次把当前质数同i的乘积筛掉
第一次出现i%primes[j] == 0发生时意味着primes[j]一定是i的最小质因子，那么primes[j]也一定是primes[j]*i的最小质因子
若我们没有枚举到i的任何一个质因子，说明primes[j]一定小于i的所有质因子，所有primes[j]也一定是primes[j]*i的最小质因子
对于一个和数x，假设pj是x的最小质因子，当i（一定会）枚举到x/pj时，就会把x筛掉

线性筛法为什么是线性的？

每个数都只有一个最小质因子，每个数也只用最小质因子来筛，所以每个数只会被筛一次，所以是线性的。不加break就可能重复筛。

约数

求所有约数

试除法+优化

vector<int> get_divisors(int n){
    vector<int> res;
    for(int i=1;i<=n/2;i++){
        if(n%i == 0){
            res.push_back(i);
            if(i!=n/i) res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

求一个数的约数个数

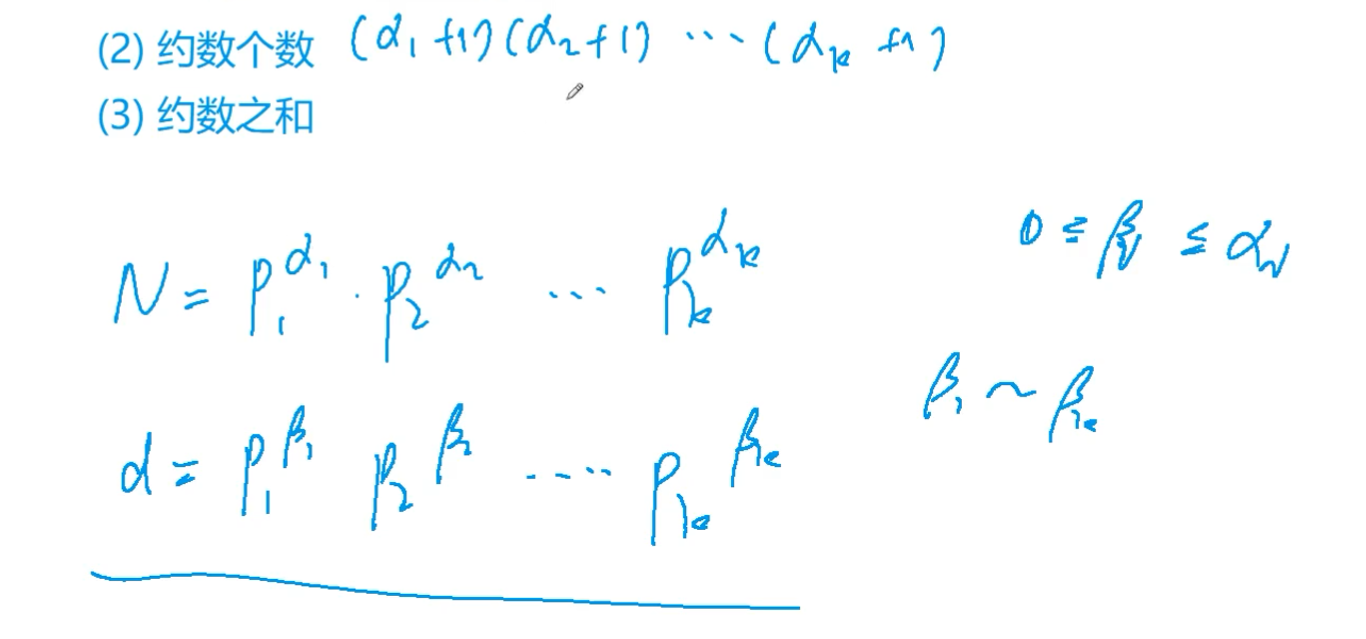
n的每一个约数d就和我们从 $到$ 的一种选法一一对应，所以约数个数为所有选法数量：$(\alpha_1+1)(\alpha_2+1)…(\alpha_{k-1}+1)(\alpha_k+1)$

```



**求一个数的约数之和**

<img src="https://raw.githubusercontent.com/coelien/image-hosting/master/img/202206251729585.png" alt="image-20220625172930529" style="zoom:50%;" />

每个约数均不相同，且是选法数量之一。

`while(a--) t = t*p+1`可以方便的求等比数列的和，其中a为指数，p为底数，也可以用公式做（尝试）

**求最大公约数**

> 辗转相除法

核心：**（a，b）= （b，a mod b)**

```c++
int gcd(int a,b){
    return b ? gcd(b,a mod b) : a;
}

欧拉函数

概念：

为1~n中与n互质的数的个数

欧拉公式：

首先对n分解质因数 $p_1^{\alpha_1}p_2^{\alpha_2}…p_k^{\alpha_k} $，根据公式即可计算出结果$ \phi(n) = n(1-1/p_1)(1-1/p_2)…*(1-1/p_k) $

证明：

使用容斥原理可以证明

从1~n中去掉
加上所有的倍数
减去所有$pipjpk$的倍数
以此类推

某些情况下，需要求出1~n中每一个数的欧拉函数

筛法求欧拉函数 O(n)

void get_eulers(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]) {
            primes[cnt++] = i;
            phi[i] = i-1;
        }
        for(int j = 0;primes[j] <= n/i ; j++){
            st[primes[j]*i] = true;
            if(i%primes[j] == 0) {
                phi[primes[j]*i] = primes[j]*phi[i];
                break;
            };
            phi[primes[j]*i] = (primes[j]-1)*phi[i];
        }
    }
}

应用：欧拉定理

若a与n互质，

注：等于号代表同余

欧拉定理的特例：费马小定理

若n为质数，假设a与n互质，那么有

快速幂

在O(log k)的情况下快速地求出的结果。

把拆成若干个预处理出来的数的乘积的形式（用2进制表示即可），即把k换成2进制即可。

typedef Long Long LL;
int qmi(int a , int k, int p){
    int res = 1;
    while(k){
        if(k&1) res = (LL)res*a%p;
        k>>=1;
        a=(LL)a*a%p;
    }
}

快速幂求乘法逆元

其实本质上就是一个快速幂

证明：

希望把除法变乘法：

左右两边同乘以b：

因而

之后可以用费马定理来解决，但注意m要为质数，且b与m互质

因而

所以b的模m的逆元为

扩展欧几里得算法

裴蜀定理

有任意一对正整数a、b，那么一定存在整数x、y，使得ax+by = gcd(a,b)

注：x，y可取负整数

解决什么问题

为裴蜀定理构造解

int ext_gcd(int a, int b, int &x, int &y){
     if(!b){
         x = 1,y=0;
         return a;
     }
     int ans = ext_gcd(b,a%b,y,x);
     y -= a/b *x;
     return ans;
}

简单应用：求解线性同余方程

等价于，所以若(a,-m)|b成立则有解，可以用扩展欧几里得算法算出x；否则无解

中国剩余定理

求解一元线性同余方程组

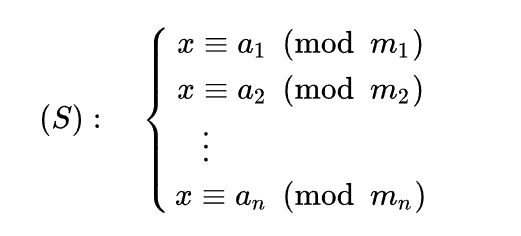
通解的构造方法：

求逆元ti可以用扩展欧几里得算法解出：

通解构造的正确性可通过带入法进行验证。

高斯消元

线性代数相关知识

一般可以再O(n^3)的时间复杂度内，求解n个方程n个未知数的多元线性方程组。

解的情况

无解：通过行变换推出0=非0，矛盾
无穷多组解：0=0，n个未知数，n-1个方程
唯一解：完美阶梯形

注：初等行变换不改变方程组的解，而且可以将方程组变为上三角的形式：

算法流程

枚举每一列，找出绝对值最大的这一行
将这行换到上面去
将该行第一个数变为1
将下面所有行的当前列消成0
若有唯一解，那么用消元法即可得到解

double a[N][N] ;
int gauss(){
    int c,r;
    for(int i=r;i<n;i++){
        
    }
}

组合数

公式法

由公式，可以计算出组合数：

int p;
int C(int a, int b){
    int res = 1;
    for(int i=1,j=a;i<=b;i++,j--){
        res = res*j % p;
        res = res *qmi(i,p-2) % p;
    }
    return res;
}

递推式法

10万组询问，a,b范围较小：1<= a,b<=2000

根据递推式，先预处理出所有的组合数（两重循环即可），到时候查表即可在O(ab)的时间复杂度下完成计算。

预处理公式法

1万组询问，a,b范围适中：1<=a,b<=1e5

根据公式，预处理出中间的一步:阶乘。用fact[i]表示i! mod 10^9+7，infact[i]表示 mod 10^9+7

也可以用查表的方式O(NlogN)来求

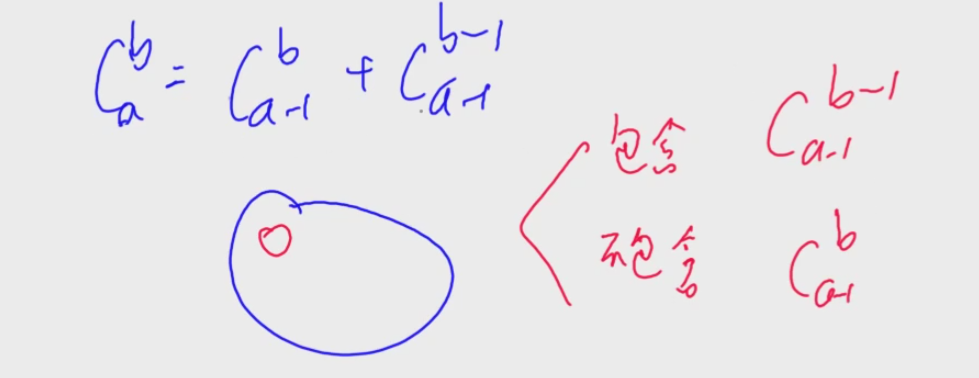
卢卡斯定理

20组询问，a,b范围巨大：1<=a,b<=10^18，1<=p<=10^5

$C^b_a = C^{b%p}{a%p}*C^{b/p}{a/p} (%p)$

算法复杂度为O()，前半部分为递归层数，后半部分为每层递归里求组合数的复杂度；

证明可参考该博客

int lukas(int a,int b){
    if(a<p && b<p) return C(a,b);
    return (LL)C(a%p,b%p) * lucas(a/p,b/p) % p;
}

分解质因数+高精度

先把分解质因数，即$p_1^{\alpha_1}p_2^{\alpha_2}…*p_k^{\alpha_k}$，之后只需要实现一个高精度乘法即可。

对每一个数分解质因数，效率较低O(NlogN)
改进：先处理出所有的质因子，再求出这个质因子的次数是多少。由公式，求p次数的方法为，先看分子里p的个数，再看分母里p的个数，差值即为真正的p的个数。那么如何得到阶乘里p的个数呢？通过下面的算法可以巧妙地计算出阶乘里p的个数：

// 暴力解法
// 分别求出1~n的质因子p的数量再相加：O(NlogN)
int get(int n, int p){
    for(int i=1;i<=n;i++){
        int t = i;
        while(t%p==0){
           t/=p;
           cnt[i]++;
        }
    }
    int res = 0;
    for(int i=1;i<=n;i++){
        res += cnt[i];
    }
}
// 优化
// 计算出阶乘里p的个数O(logN)
int get(int n, int p){
    int res = 0;
    while(n){
        res += n/p;
        n/=p;
    }
    return res;
}

卡特兰数

$C_{2n}^{n}-C^{n-1}{2n}=1/(n+1)*C^n{2n}$

应用

火车进站问题

合法括号序列问题

容斥原理

对于n个圆，计算其所占的面积，数字代表i个圆的交集的组合。

对于集合来讲，集合的个数也满足上式。

上式一共有多少项？

从n个数里挑任意多个数的方案数

所以一共有项，所以时间复杂度为

为什么是+、-、+、-？

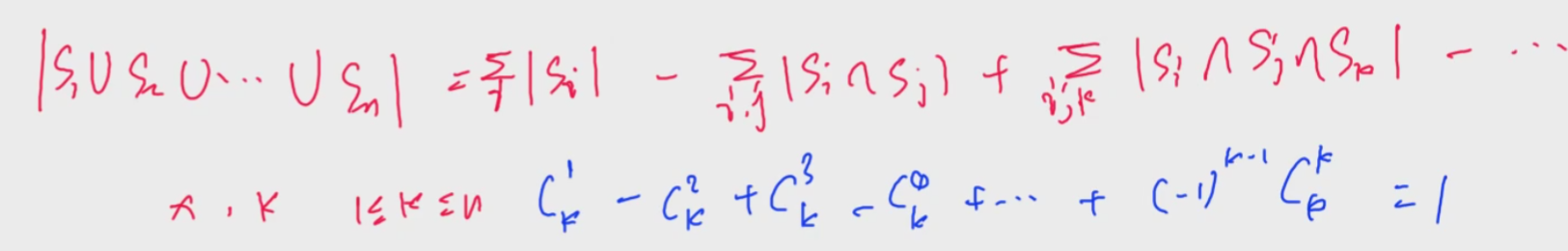
根据组合恒等式，对于集合中的某个数x，它在k个集合中出现过，它只会在右边的等式里计算一次。

实际应用

博弈论

Nim游戏

给定n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子，最后无法进行操作的人视为失败。

先手必胜状态：可以走到某一个必败状态
先手必败状态：走不到任何一个必败状态

定理：对于n堆石子(a1,a2,a3,…,an)，如果a1^a2^…^an=0，先手必败，否则先手必胜

思考题：台阶Nim游戏

集合-Nim游戏

局面（状态）

SG（终点）=0；

SG（x）=mex{SG(y1),SG(y2),…,SG(yk)};

若SG(x)!=0，必胜，否则必败。