coding笔记：最短路

最短路

难点在于建图，而不在算法的原理上：给你一个背景，如何把问题抽象成最短路，侧重于实现思路，而不侧重于原理

常见的最短路问题

单源最短路

一个点到其他点的所有最短路

所有边权都是正数

n为点数，m为边数

朴素dijkstra算法：O(n^2)

如果是稠密图(m ~ n^2)，尽量使用朴素dijkstra算法，其算法流程如下：

1. 初始化：dist[1]=0, dist[i] = 正无穷，S=当前已确定最短路的点的集合{}
2. n次迭代：for i : 1~n 在没有确定的点中找到最小值，将距离最短的点加入S，使用t更新其他点的距离

因为是稠密图，所有推荐用邻接矩阵来存，存在重边的话，就只保留距离最短的那条边即可

int 

堆优化版的dijkstra算法：O(mlogn)

如果是稀疏图(m ~ n)，用邻接表来存，那么应该用堆优化版dijkstra算法

存在负权边

若能求出最短路，对应路径内中一定没有负权回路

Bellman-Fold ：O(nm)

外层循环n次，内层循环所有边，一个比较朴素的算法。

实际意义：迭代k次，dist[]存的是不超过k条边的最短路距离，若第n次依然有更新，说明存在负权回路

SPFA： 一般O(m) ，最坏O(nm)

没有负环就可以用SPFA，99%情况下都可以用。

若cnt[x]>=n，说明存在负环

多源汇总最短路

不止一个起点，任选两个点，从其中一个点到另一个点的最短路问题

Floyd算法：O(n^3)

采用动态规划的思想：d[i,j]存储所有边，floyd算法包含三重循环：

• 第一重：k从1到n
• 第二重：i从1到n
• 第三重：j从1到n:
  • d(i,j) = min(d(i,j), d(i,k) + d(k,j))

总结

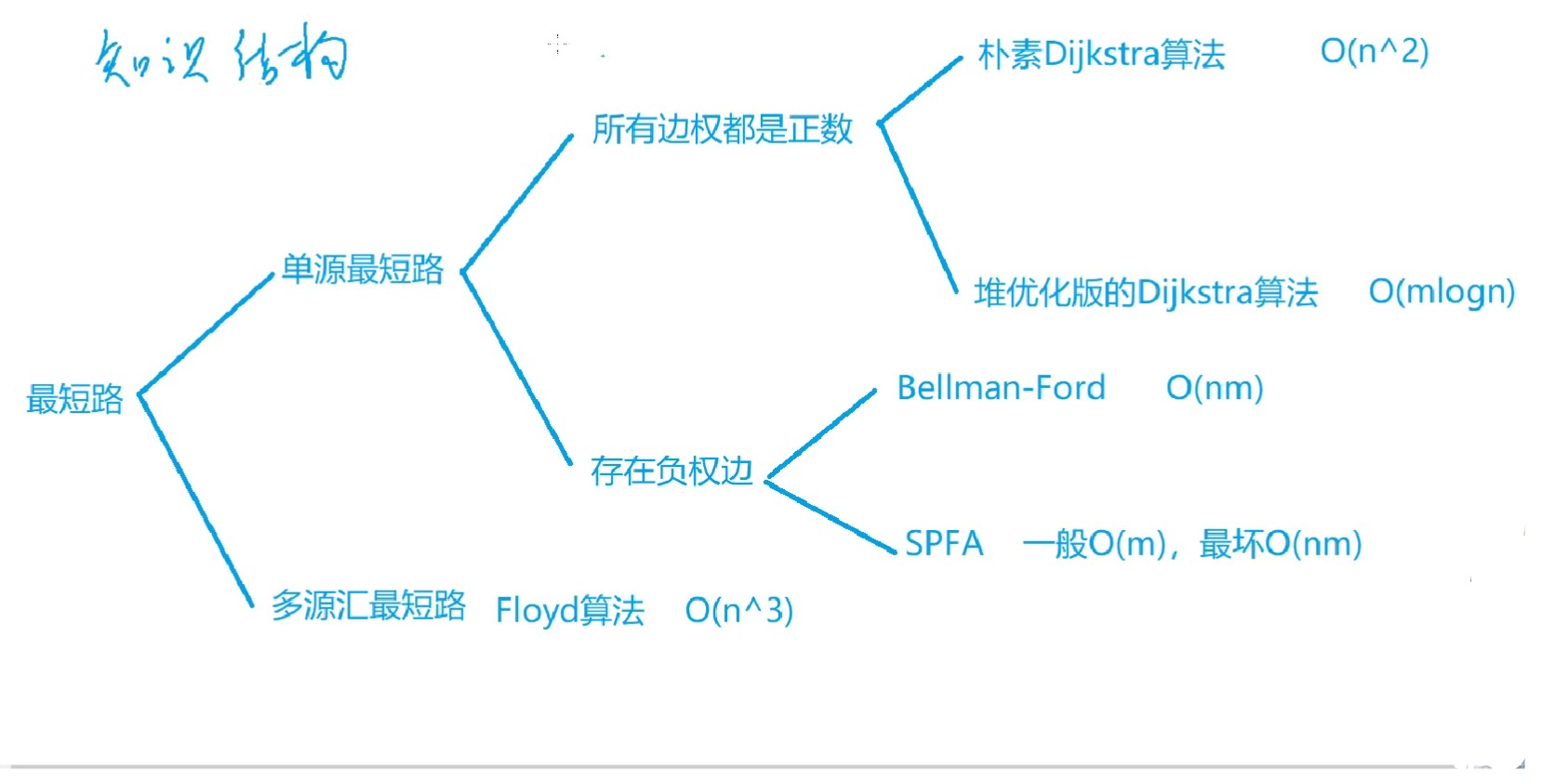
最短路问题总结见下图：(参考acwing视频)