coding笔记： 树状数组和线段树

树状数组和线段树

树状数组

核心应用：动态快速地求前缀和 O(logn)

• 单点修改：在某个位置上加上一个数（修改这个数）
• 区间查询：求某一个前缀和
• 区间修改：配合差分思想转换为已知问题
• 单点修改：配合差分思想转换为已知问题

思考：为什么不直接使用前缀和数组直接查表？

• 不支持修改操作、或者说修改操作复杂度极高(O(n))
• 在所有操作里，如果修改操作多，那么树状数组会很高效

算法思路

• 本质是一维数组。

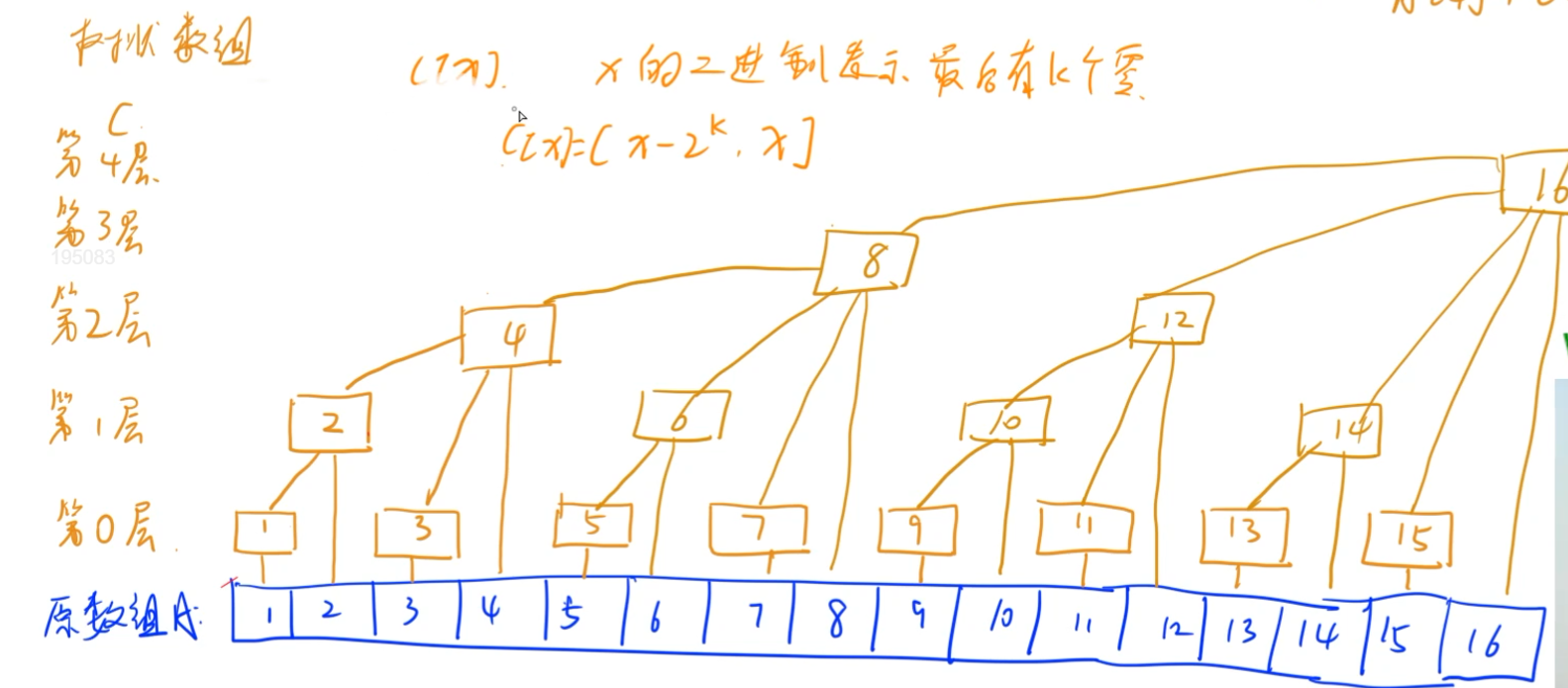
思考：如何计算x的二进制表示有多少个0？

• lowbit(x) = x & -x = 2^k（二进制的最后一位1）

c[x]存的是什么？

• 存的是：(x-lowbit(x)，x]之和

实现代码

• 求前缀和

int res = 0;
for(int i=x; i>0;i-=lowbit(x)) res+=c[i];
return res;

• 更新

for(int i=x; i<=n; i+=lowbit(i)) c[i]+=v;

当前结点x的父节点就是x+lowbit(x)

线段树

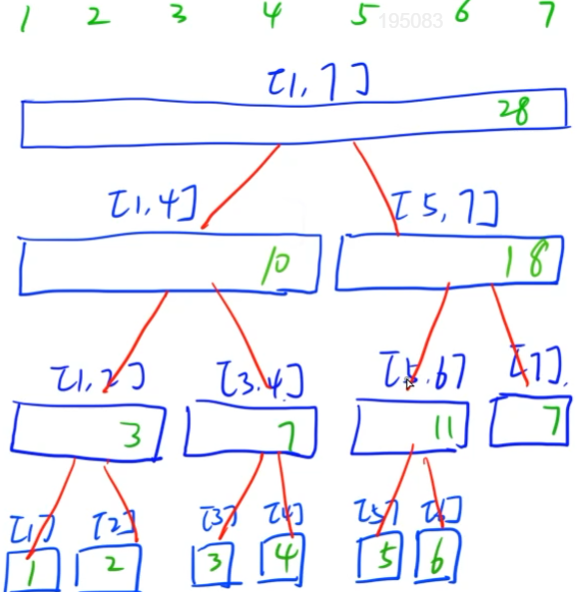
线段树操作

对于维护总和的线段树来说，它有两个操作：

• 单点修改 **O(logn)**：递归修改所有和x相关的结点，回溯时维护总和
• 区间查询 **O(logn)**：不断往下递归，直到递归到目标区间完全包含它（区间或是叶节点）为止

线段树存储：

和heap是一种存储方式，假设有n个数，最多不超过4n个结点

当前结点下标是x:

• 父节点下标为 [x/2] x>>1
• 左儿子下标为 2*x x<<1
• 右儿子下标为 2*x+1 x<<1 | 1

核心函数：

• pushup：用子结点信息更新当前结点信息（可写到其他函数内部）
• build：在一段区间上初始化线段树
• modify：修改
• query：查询