coding笔记：贪心算法

贪心算法

证明困难，没有常用的套路

对于区间问题：

• 左端点排序
• 右端点排序
• 双关键字排序

如上图，局部极值不一定是权重最优解，因此只有一个问题是单峰的，才可以用贪心算法来解

区间选点

算法思路

1. 将每个区间按右端点从小到大排序
2. 从前往后依次枚举每个区间：
   • 如果当前区间中已经包含选点，则直接pass
   • 否则，选择当前区间的右端点

算法证明

1. Ans <= Cnt

整个算法流程保证了，选出Cnt个点的方案是合法方案，因此由上面的不等式

2. Ans >= Cnt

选出Cnt个点，实际上是找出了Cnt个不重叠区间，因此选点方案的最小数量至少为Cnt，即Ans>=Cnt

由上，即可证明Ans==Cnt

最大不相交区间的数量

算法思路

做法和上一题完全一样

算法证明

Ans是最大不相交区间的数量，Cnt是算法选择的点的数量（Cnt个不重叠区间）

1. Ans >= Cnt

选出Cnt个点的方案一定是合法方案，所以Ans>=Cnt

2. Ans <= Cnt

反证法：假设Ans>Cnt，意味着我们可以选出比Cnt更多个互不相交区间；由每一个区间至少包含一个我们选择出来的点，那么根据假设我们至少要选出来Ans个点，这与实际我们最少选出Cnt个点相矛盾，因此Ans <= Cnt

区间分组

算法思路

1. 将所有区间按左端点从小到大排序
2. 从前往后处理每个区间
   • 判断能否将其放到某个现有的组中
     • 不能放入(不存在一个组可以放入)，则开新组，然后再将其放进去；
     • 可以放入：L[i] > Max_r，将其放进去，并更新当前Max_r

算法证明

Ans是相互补充的的区间的组的最小组数，cnt是算法的组数

1. Ans <= Cnt

按照算法得到的组数一定是一种合法的方案，而Ans是方案的最小值，因此Ans <= Cnt

2. Ans >= Cnt

算法开新组的条件是该区间与每个组都有交集，因此Cnt其实是最少开的组的数量（不能更少，否则会有交集），因此Ans >= Cnt

区间覆盖问题

算法思路

1. 将所有区间按照左端点从小到大排序
2. 从前往后依次枚举每个区间，在所有能覆盖开始点的区间中选择右端点最大的区间，若右端点>end，算法退出
   • 若能选出，将start更新成右端点最大值
   • 若找不到满足对应条件的区间，输出-1

霍夫曼树-合并果子

算法思路

叶节点到根结点一共有多长，对叶节点就要加多少遍。因此每次挑两个值最小的点相合并，他们深度一定最深，可以互为兄弟。

算法证明

1. 深度最深：假设最小的两个点为a,f，那么b,f交换后一定收益为正

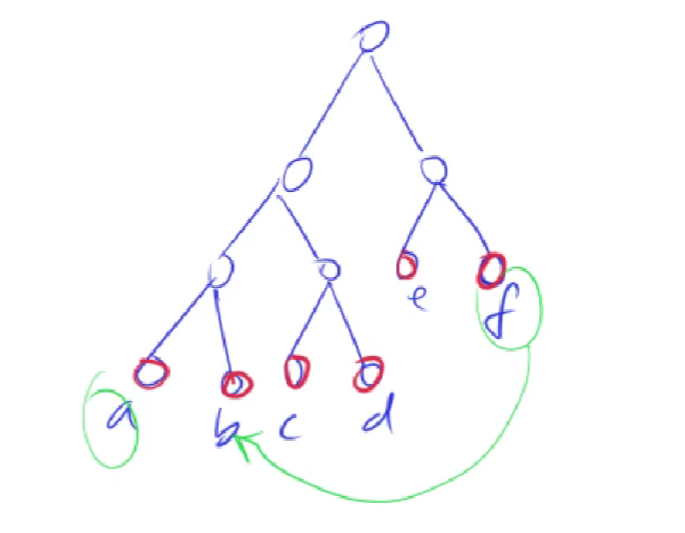
2. 可以互为兄弟：a,b,c,d顺序可以交换，不影响全局最优解

3. 合并剩下n-1个果子的最优解一定是合并n个果子的最优解吗？

   即f(n) = f(n-1)+a+b成立吗？

   因为合并果子一定可以先合并最小两个点作为最优解，所以对于所有方案都可以把（a+b）去掉不影响最值，因此原问题就可以变为n-1个点的huffman问题，所以合并剩下n-1个果子的最优解一定是合并n个果子的最优解

排序不等式

可能会爆int，所以用Long Long来做

算法思路

按照从小到大的顺序排队，总时间最小

算法证明

调整法

若不是排好序的，那么一定存在ti>ti+1,若我们将ti和ti+1交换位置，那么交换前比交换后多了ti-ti+1>0，也就是说交换完后总时间就会降低。

绝对值不等式

算法思路

按照从小到大排序，取中位数

算法证明

分组法

只要x位于a,b之间，就可以取到最小值。分组后对每一个组都可以取到最小值，同时取即是总共的最小值，即取到正中间即可。

推公式

基于不等式来证明贪心问题

算法思路

按照wi+si从小到大的顺序排，最大的危险系数一定是最小的

算法证明

只要最优解不是严格从小到大递增的，我们一定可以找到第i个位置上的牛和第i+1位置上的牛他们满足，交换完这两个牛后，我们可以证明，这两个危险系数的最大值一定会严格变小