coding笔记： 动态规划
sixwalter Lv6
  2023-08-05 11:14:26 2023-08-05 11:14      2k Words  8 Mins  

动态规划基础

理解动态规划的思考方式

从集合的角度理解DP问题

  • 状态表示 f(i,j)（存的是所有选法的集合的最大值），考虑清楚需要几维来表示我们的问题

    • 集合：每一个状态都是表明一个集合，在背包问题里表示所有选法的集合

      条件：

      • 只考虑前i个物品
      • 总体积不超过 j

    • 属性：集合的最大值，最小值，元素数量

  • 状态计算 ，如何将每个状态计算出来

    • 目标：求f(N,V)

    • 状态计算一般表示集合的划分：把当前集合划分为若干个更小的子集，使得每一个子集我们都可以由前面更小的状态计算得到

      例如f(i,j)可以包含两类：

      • 左边类是不包含第i个物品的选法
      • 右边类是包含第i个物品的选法

      实际的最大值是两类取一个max

DP问题的优化一般只是等价变形，所以写出朴素解法十分重要

DP问题一定要结合题目来理解，上面的思考方式就像是骨架，根据具体问题填补具体的血肉

背包模型

01背包问题

什么是01背包？

每件物品最多只能用一次

在背包容量的范围内如何挑选物品，让总价值最大

朴素做法

1
2
3
4
5
6
7
8
//枚举所有状态f[0,0]~f[n,m]
//其中f[0,0-m]表示考虑0件物品，总体积不超过0~m的最大价值是多少
//因此只需从1开始遍历即可
for(int i=1;i<=n;i++)
    for(int j=0;j<=m;j++){
        f[i][j] = f[i-1][j];
        if(j>=v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]] + w[i]);
    }

一维做法

第i层的状态只依赖于第i-1层；不超过的总体积j只依赖于<=j的状态，因此可以优化到一维来做

1
2
3
4
5
int f[N];//直接去掉一维
for(int i=1;i<=n;i++)
    for(int j=m;j>=v[i];j--){
        f[j] = max(f[j],f[j-v[i]]+w[i]);
    }

完全背包问题

每件物品可以用无限次

解题思路

分成若干组，分成k类：

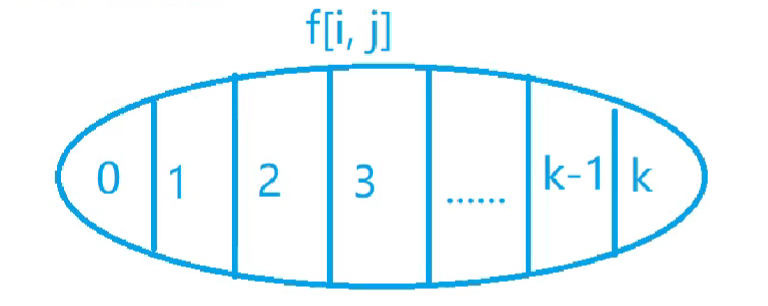
image-20220714135234544

不妨设第i个物品选了k个

曲线救国：

  1. 去掉k个物品i
  2. 求Max，f[i-1,j-k*v[i]]
  3. 再加回来k个物品i

综上，f[i,j] = f[i-1,j-k*v[i]] + k * w[i]

朴素做法

1
2
3
4
5
//最坏情况下：O(n*m^2))
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++)
        for(int k=0;k*v[i]<=j;k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

二维做法

1
2
3
4
5
6
7
8
9
//f[i,j] = Max(f[i-1][j],f[i-1,j-v]+w,f[i-1,j-2v]+2w,f[i-1,j-3v]+3w,...)
//f[i,j-v] = Max(f[i-1][j-v],f[i-1,j-2v]+w,f[i-1,j-3v]+2w,...)
//f[i,j] = Max(f[i-1][j],f[i,j-v]+w);
//优化为二维
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++){
        f[i][j] = f[i-1][j];
        if(j>=v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
    }

一维做法

完全背包问题的终极解法

1
2
3
4
int f[N];
for(int i=1;i<=n;i++)
    for(int j=v[i];j<=m;j++)
        f[j] = max(f[j],f[j-v[i]]+w[i]);

多重背包问题

每件物品最多有Si个

解题思路

枚举第i个物品选多少个，根据第i个物品选多少个来将我们所有的选法分成若干种类别：

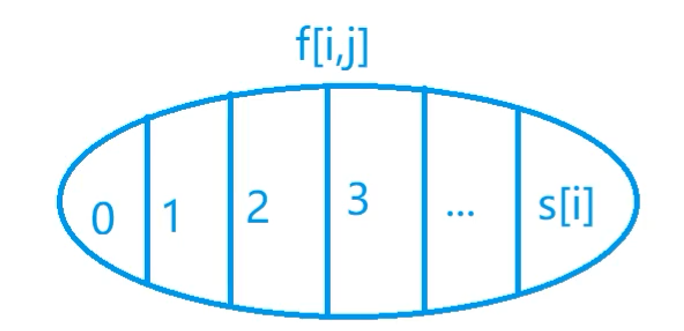
image-20220714145946121

其实就是朴素版本的完全背包问题：f[i,j] = f[i-1,j-k*v[i]] + k * w[i]

朴素版本

1
2
3
4
5
//最坏情况下：O(n*m^2))
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++)
        for(int k=0;k<=s[i] && k*v[i]<=j ;k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

优化版本：二进制优化

c++1s最多算1亿次，超过一亿次会超时

从0~s中的任何一个数都可以被拼凑出来（由1，2，4，2^k, … , c）。

将s个物品i拆分程log(s)个新的物品，新的物品只能用一次

对所有这些新出来的物品做一遍01背包即可，时间复杂度为O(N*v*log(s))

分组背包问题

状态表示的集合：只能从前i组物品中选，且总体积不大于j的所有选法

枚举第i组物品选不选，选哪个

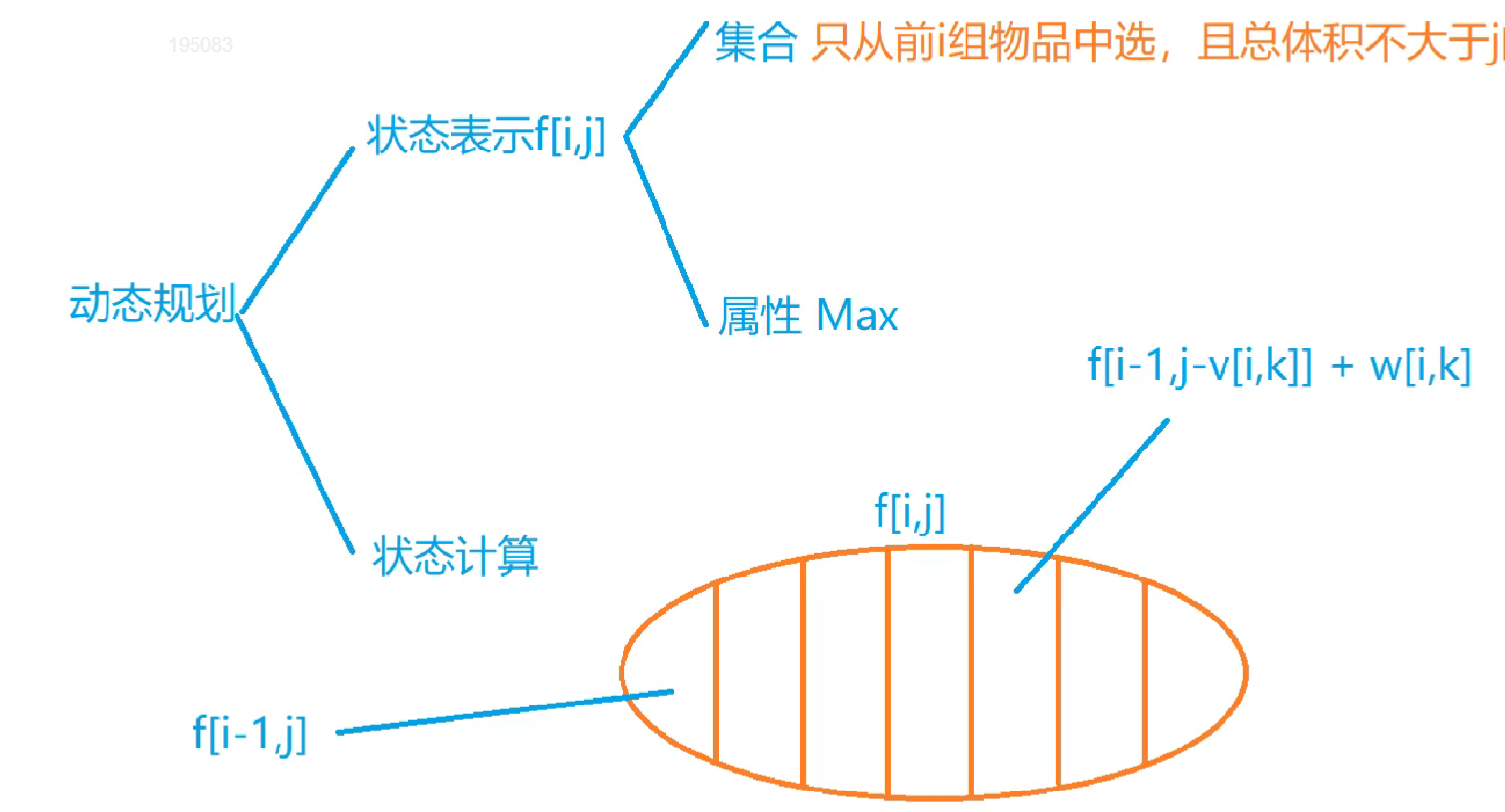
image-20220714155045511

朴素解法

1
2
3
4
5
6
7
for(int i=1;i<=n;i++)
    for(int j=0;j<=m;j++){
        f[i][j] = f[i-1][j];
        for(int k=0;k<s[i];k++){
            if(j>=v[i][k]) f[i][j] = max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
        }
    }

优化解法

1
2
3
4
5
6
int f[N];//直接去掉一维
for(int i=1;i<=n;i++)
    for(int j=m;j>=0;j--)
    	for(int k=0;k<s[i];k++){
            if(j>=v[i,k]) f[j] = max(f[j],f[j-v[i,k]]+w[i,k]);
        }

线性DP

数字三角形

状态表示

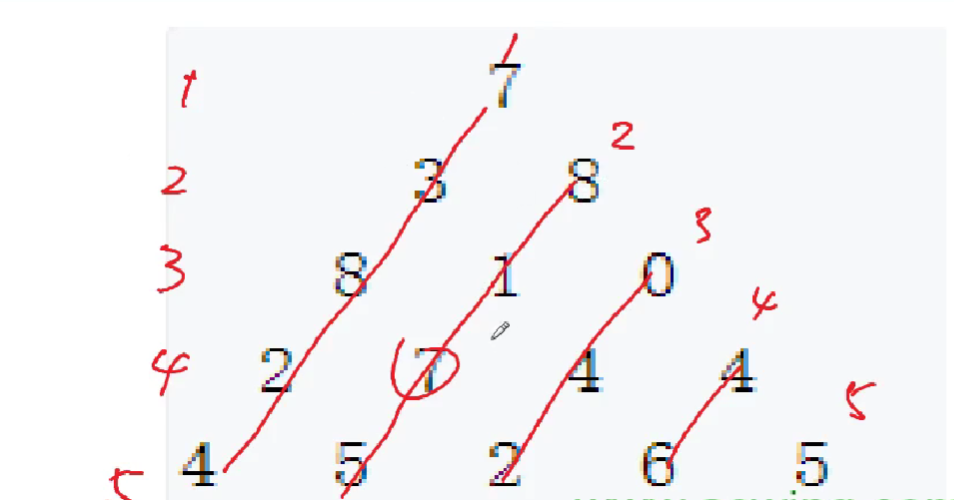
image-20220718102743701
  • 集合：从顶点到(i,j)的所有路径
  • 属性：MAX

状态计算

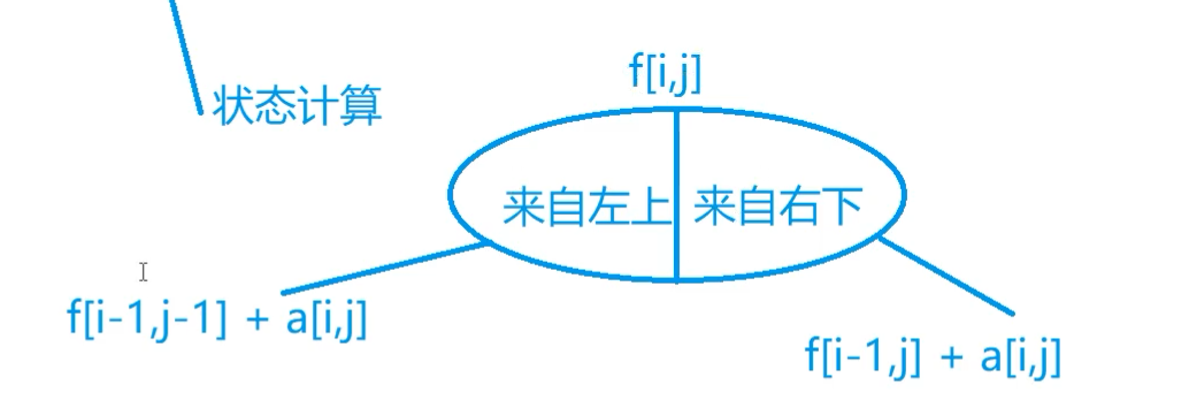
image-20220718103338018

复杂度：状态数量*转移数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const int  N = 510,inf = -1e9;
int f[N][N];
int d[N][N];
void digi_Tran_Test(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            scanf("%d",&d[i][j]);
    for(int i=0;i<=n;i++)
        for(int j=0;j<=i+1;j++)
            f[i][j]= inf;
    f[1][1] = d[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++){
            f[i][j] = max(f[i-1][j-1],f[i-1][j])+d[i][j];
        }

    int res = inf;
    for(int i=1;i<=n;i++)
        res = max(res,f[n][i]);
    cout<<res<<endl;

}

最长上升子序列

可以按照顺序跳着选择

状态表示

  • 集合：所有以第i个数为结尾的数值上升的子序列
  • 属性：子序列的最大长度

状态计算

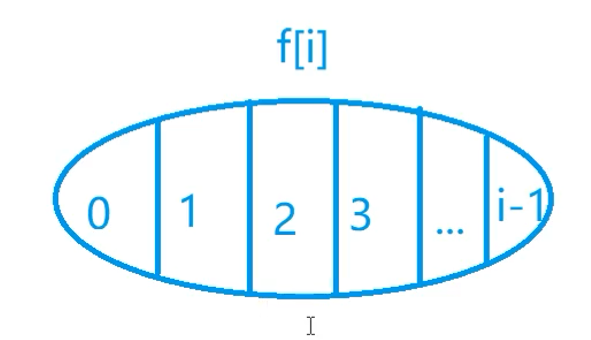
image-20220718105358393

朴素版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int M = 1010;
int sta[M];
int sq[M];
void maxLenIncSubTest() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&sq[i]);
    for(int i=1;i<=n;i++) {
        sta[i] = 1;
        for (int j = 1; j < i; j++) {
            if(sq[j]<sq[i])
                sta[i] = max(sta[i],sta[j]+1);
        }
    }
    int res = 0;
    for(int i=1;i<=n;i++)
        if(res < sta[i]) res = sta[i];
    cout<<res<<endl;
}

优化版

最长公共子序列

状态表示

  • 集合：所有由第一个序列的前i个字母，和第二个序列的前j个字母的构成的公共子序列
  • 属性：公共序列的最大值

状态计算

求max是可以重复的，只要不漏掉某一元素即可

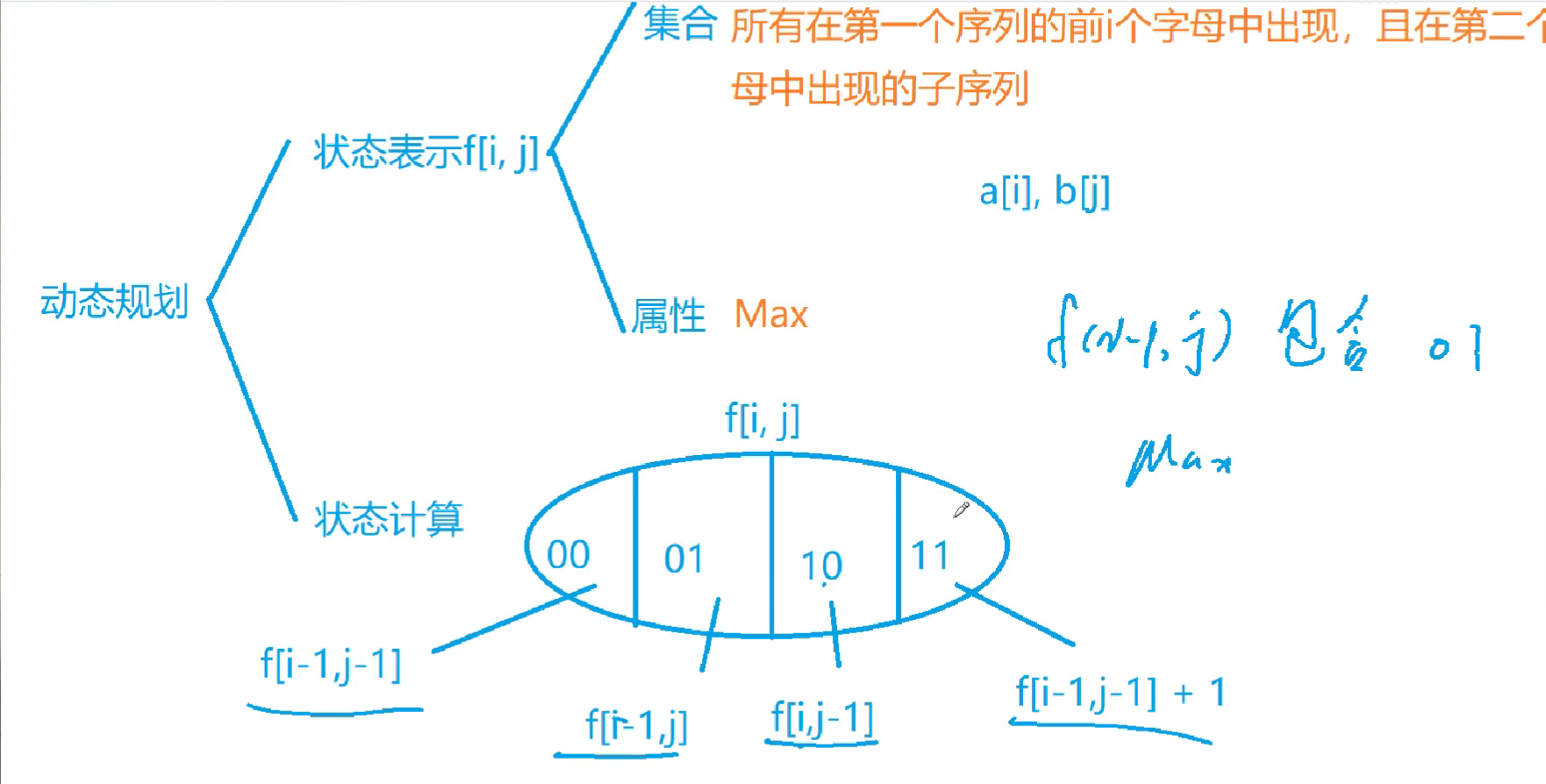
image-20220718143637328 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int M = 1010;
char a[M];
char b[M];
int st[M][M];
void maxCommenSubTest(){
    int n,m;
    cin>>n>>m;
    scanf("%s",a+1);
    scanf("%s",b+1);
    // A中前i个字符和B中前j个字符所构成的公共子序列的集合
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            st[i][j] = max(st[i][j-1],st[i-1][j]);
            if(a[i]==b[j]) st[i][j] = max(st[i][j],st[i-1][j-1]+1);
        }
    cout<<st[n][m]<<endl;
}

编辑距离

区间DP

不同的合并顺序需要的体力是不同的

状态表示

  • 集合：从第i堆石子到第j堆石子合并成一堆石子的合并方式
  • 属性：Min

状态计算

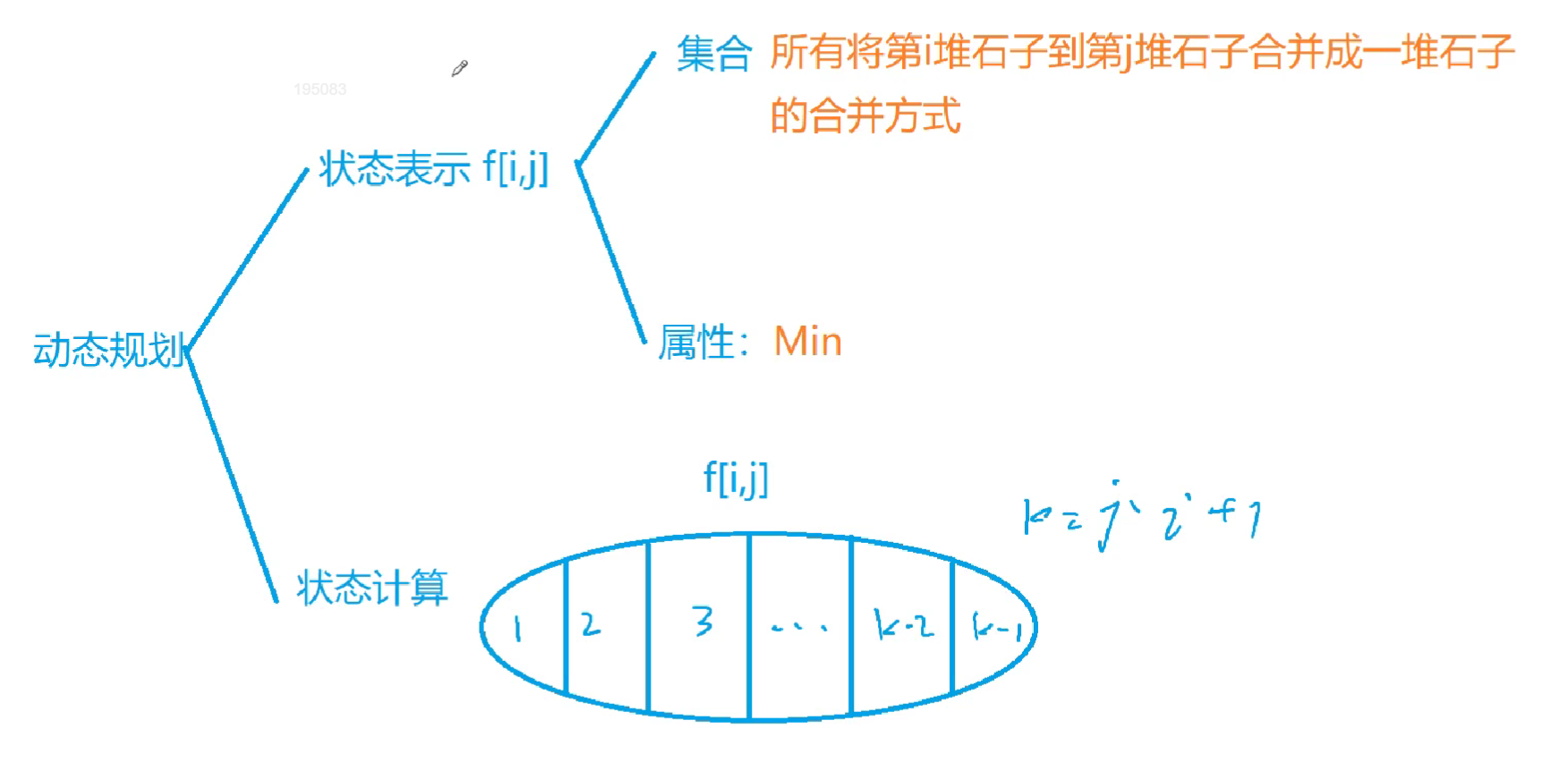
image-20220718151622394

按区间长度从小到大枚举

计数类DP

整数划分问题

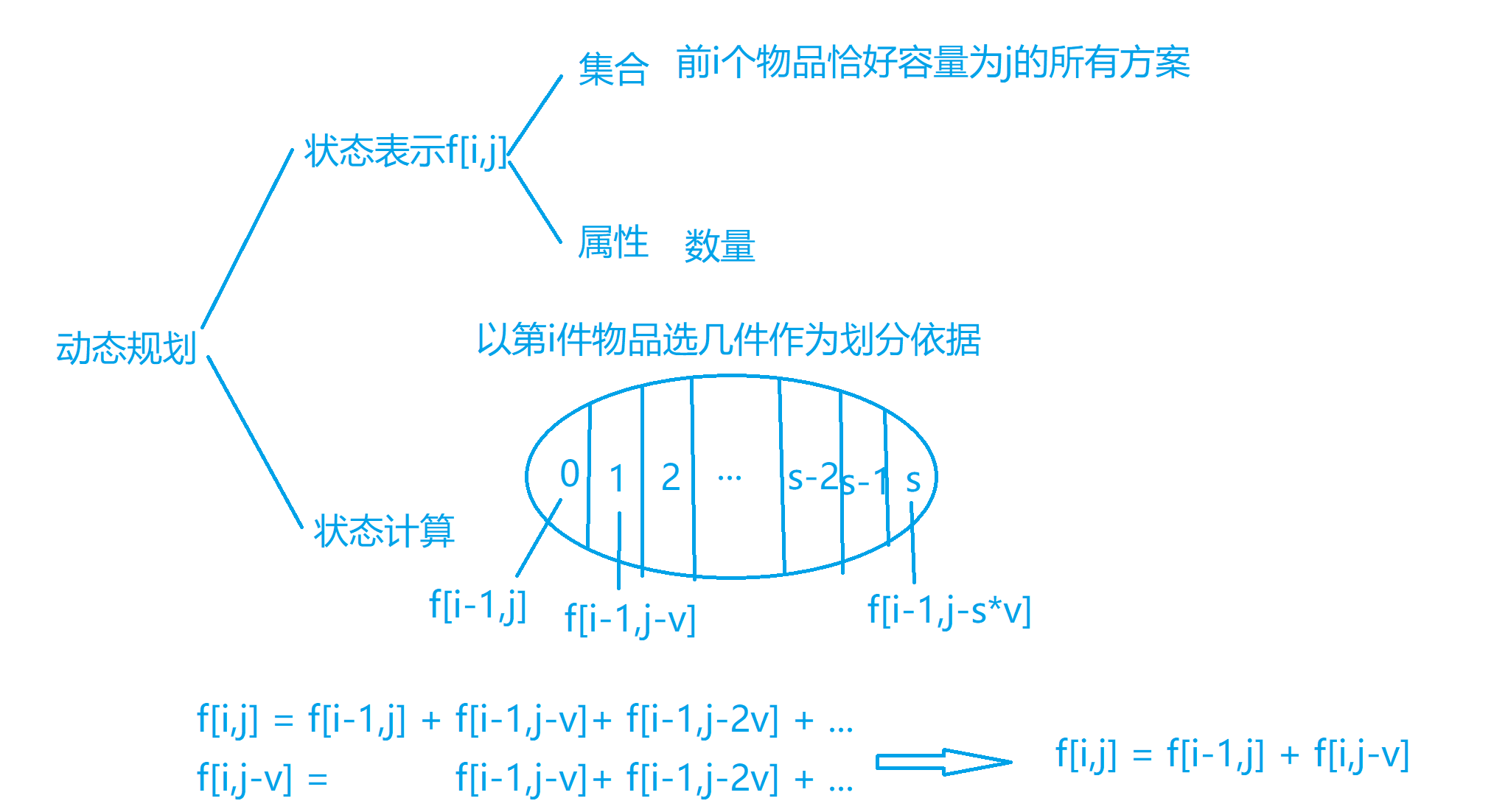
image-20220725184543921

数位统计DP

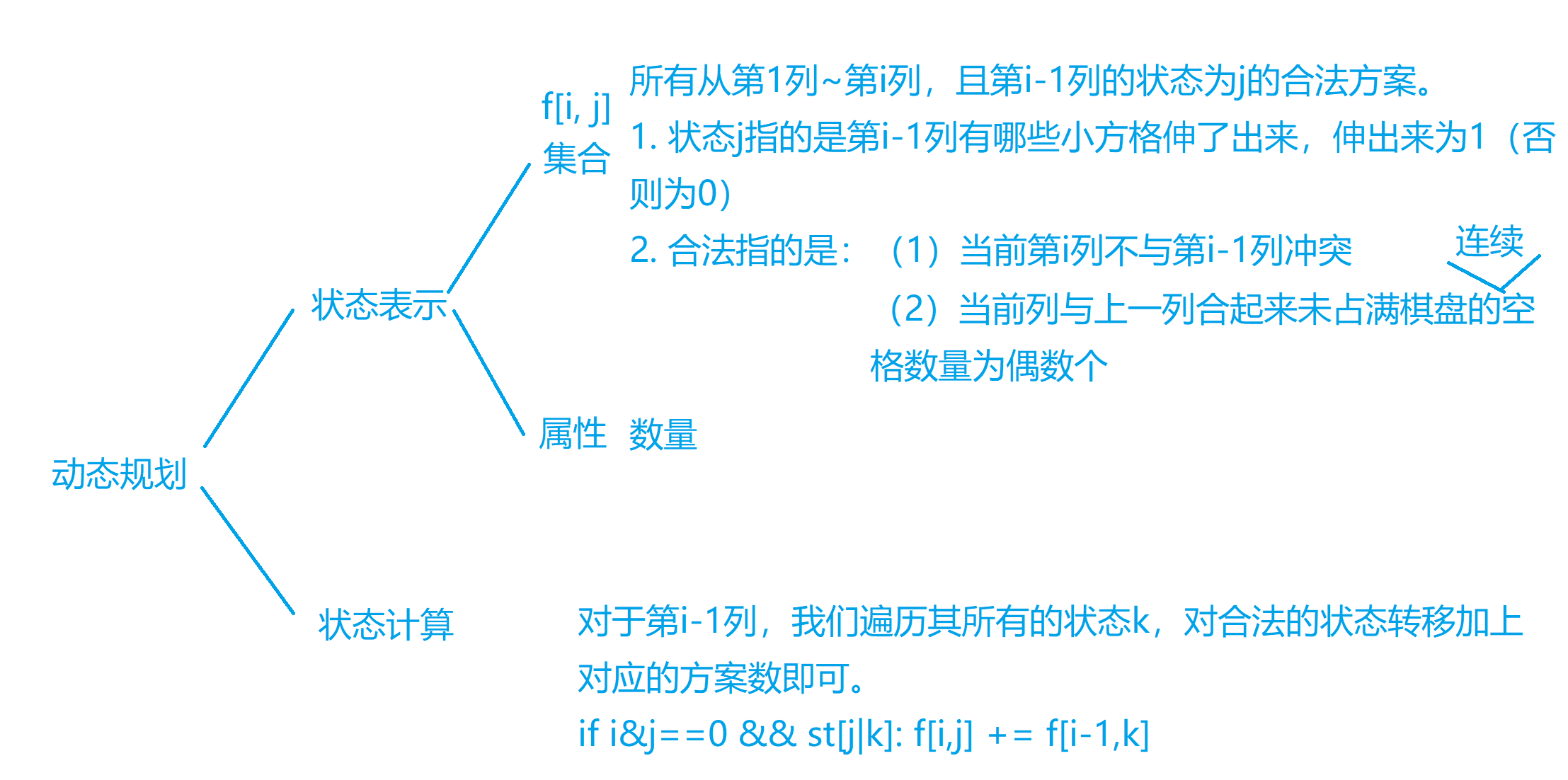
状态压缩DP

使用整数来表示状态，把这个整数看作是二进制数，每一位是0是1代表不同的情况，因此位数(n)最多取到20位（1e6种状态）

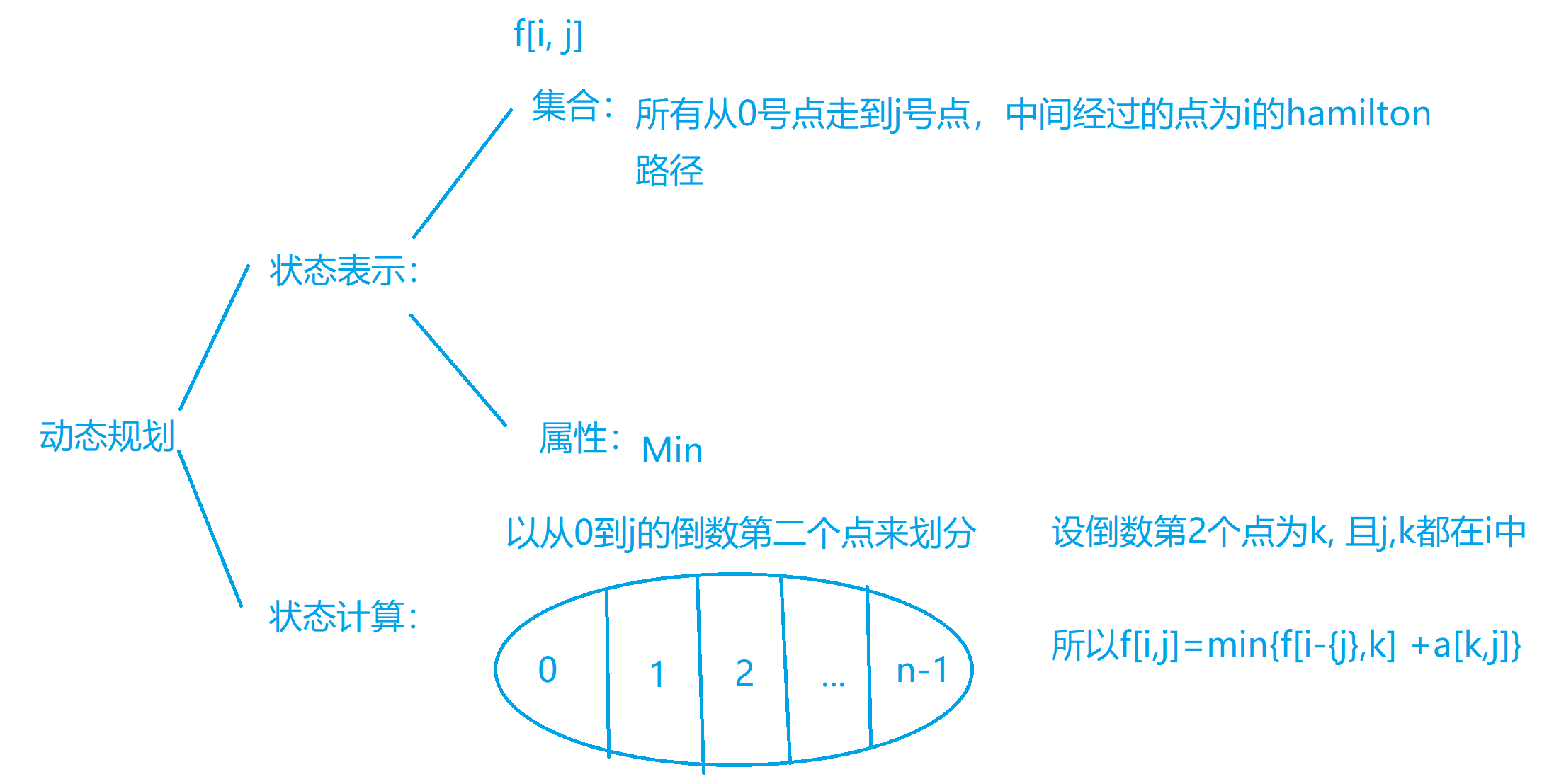
image-20220728203213749 image-20220729105012006

树形DP

接受了之后思维跨度就不高

记忆化搜索

每一道动规题都可以用递归的方法做

  • Post title：coding笔记： 动态规划
  • Post author：sixwalter
  • Create time：2023-08-05 11:14:26
  • Post link：https://coelien.github.io/2023/08/05/coding-solution/DP/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.
 Comments