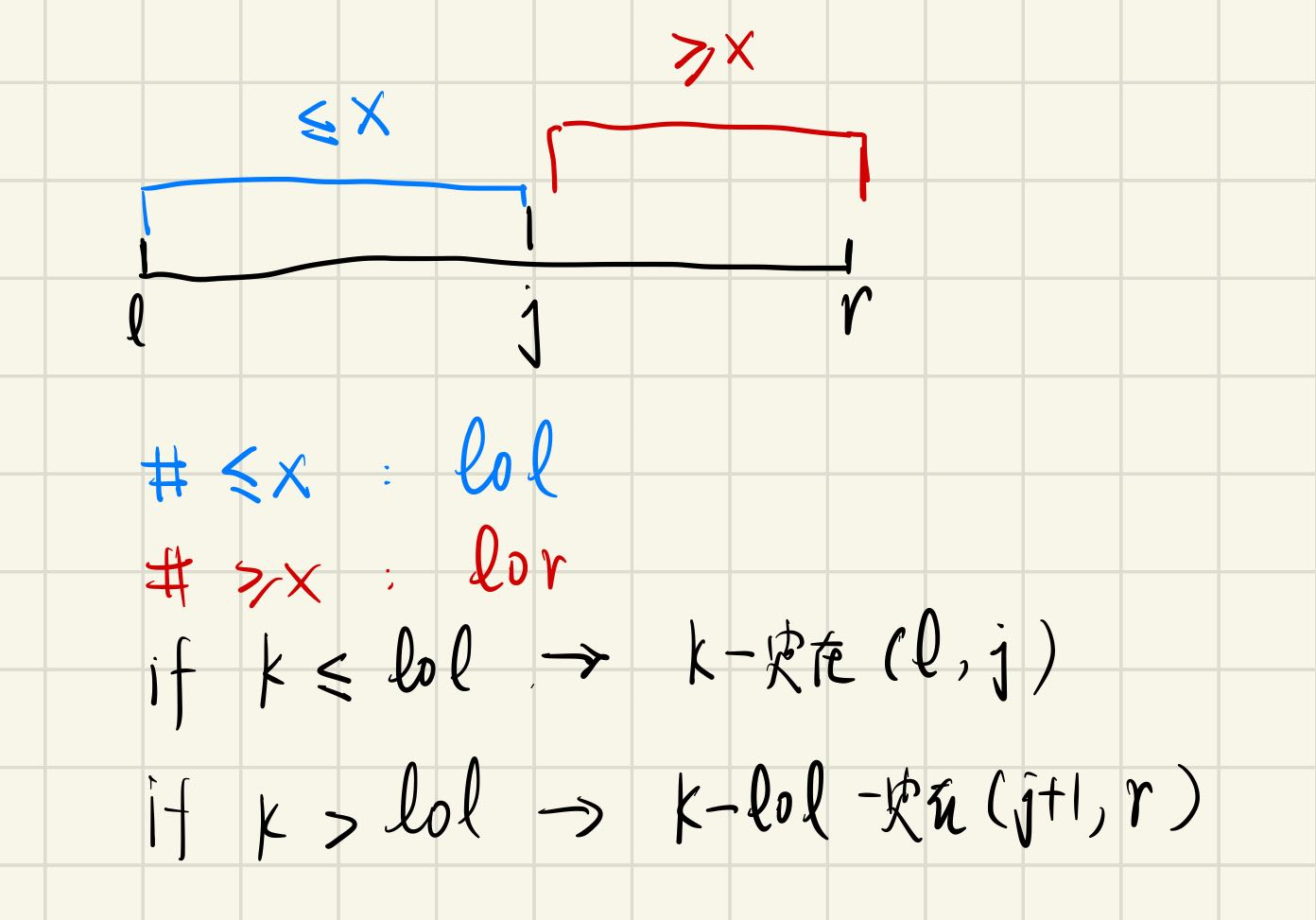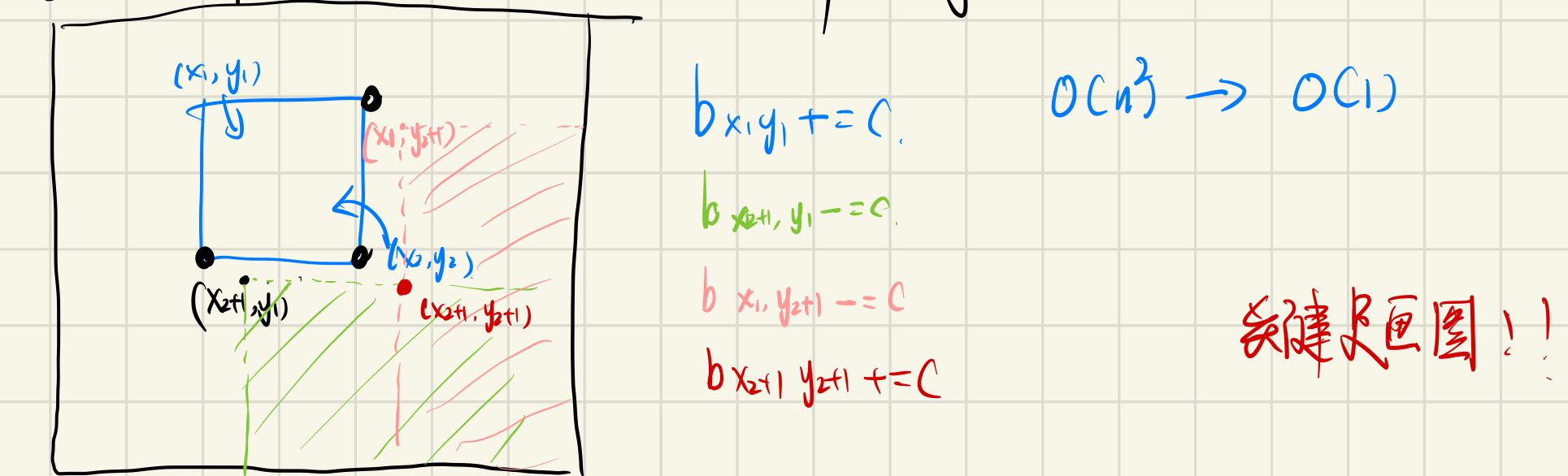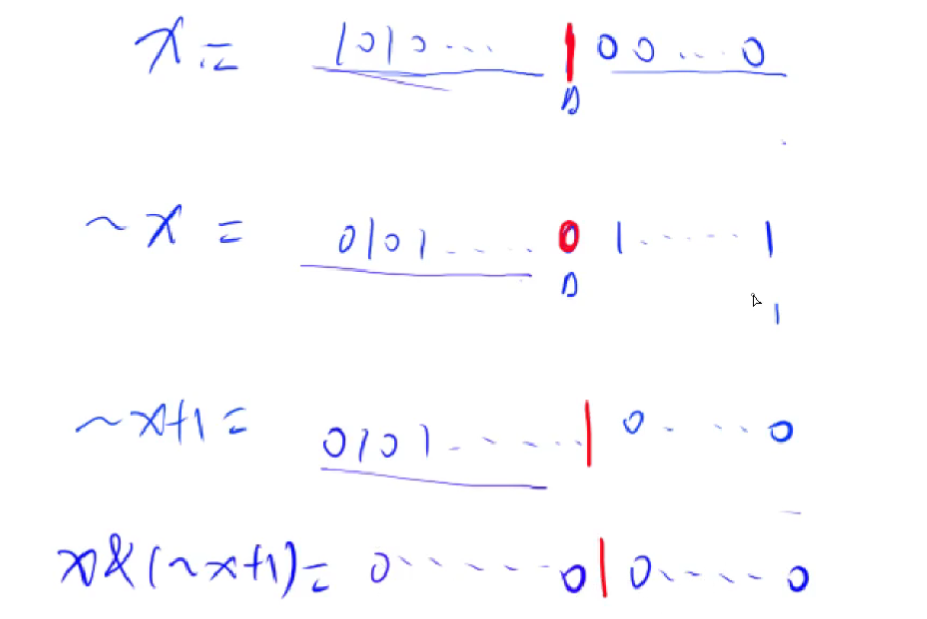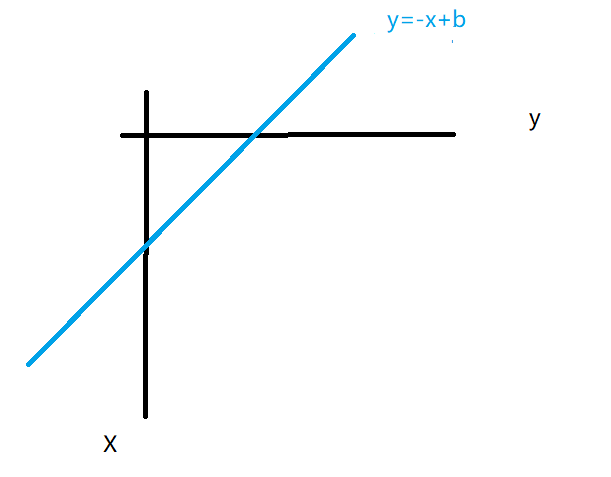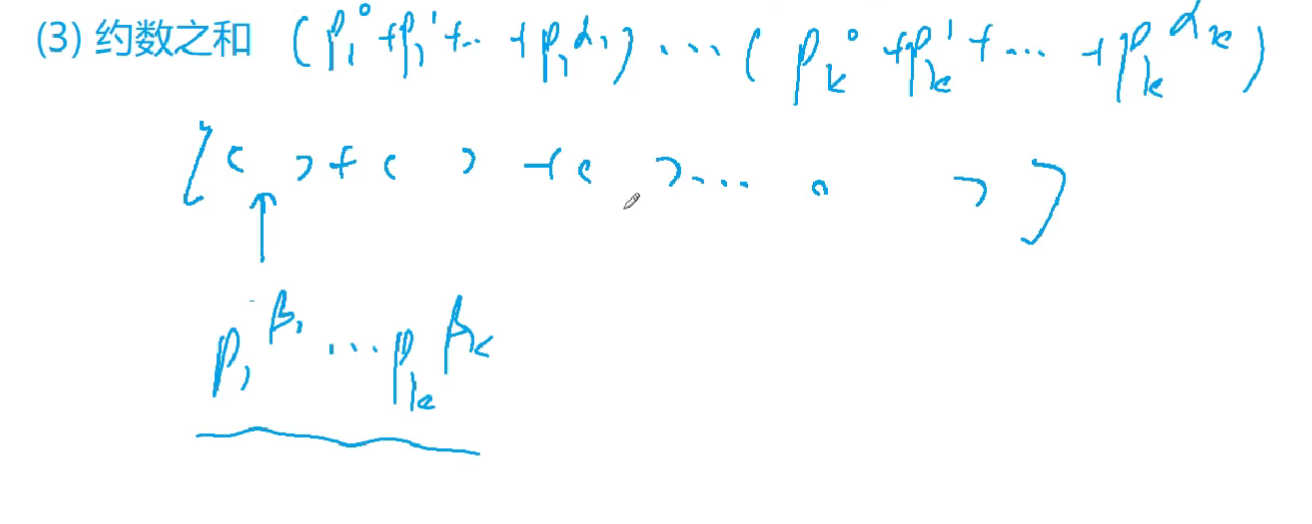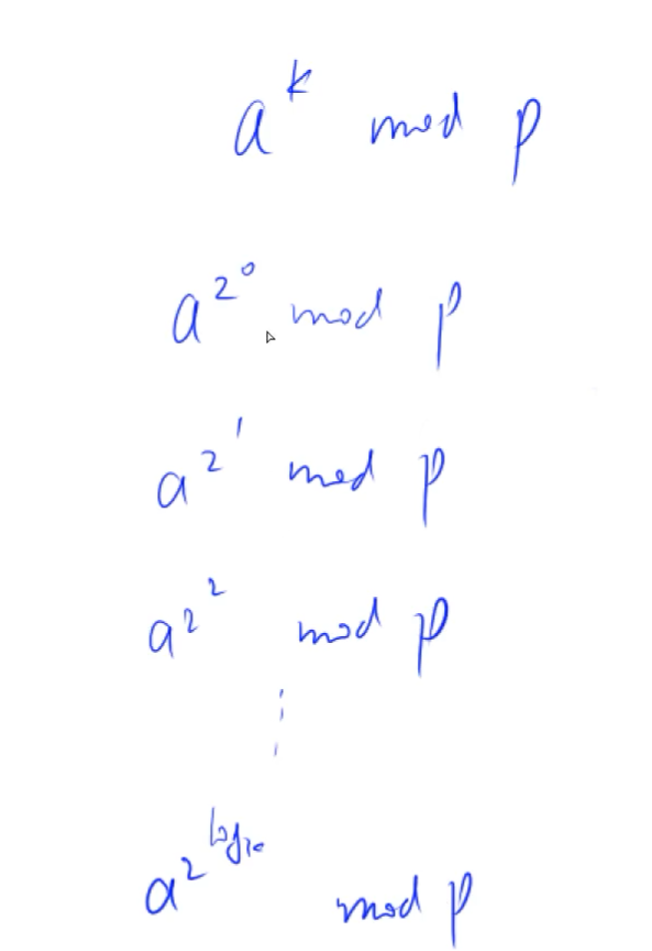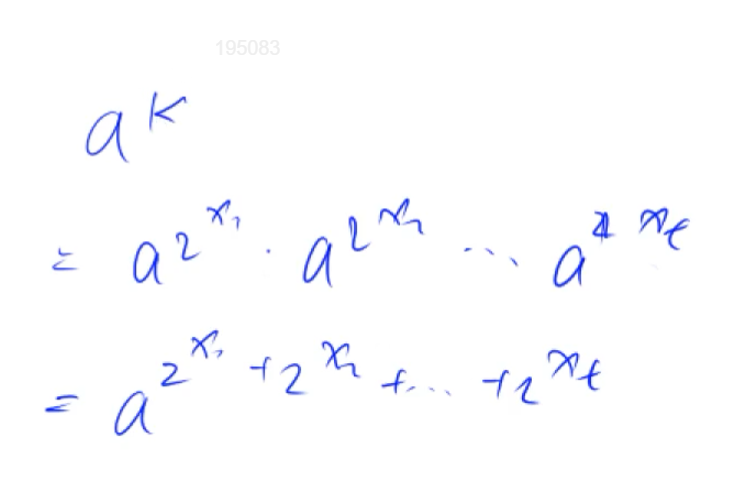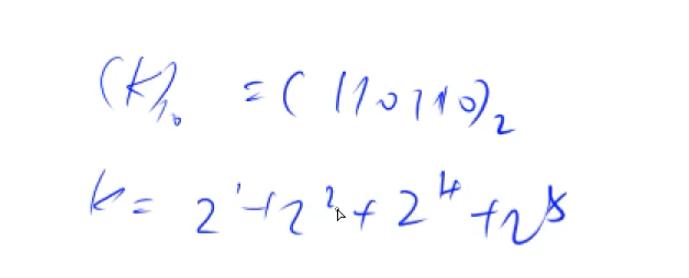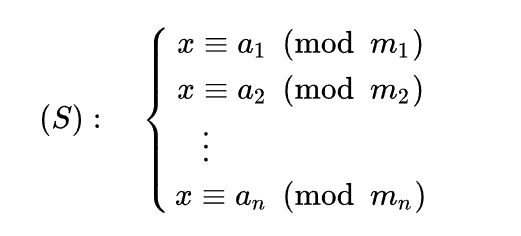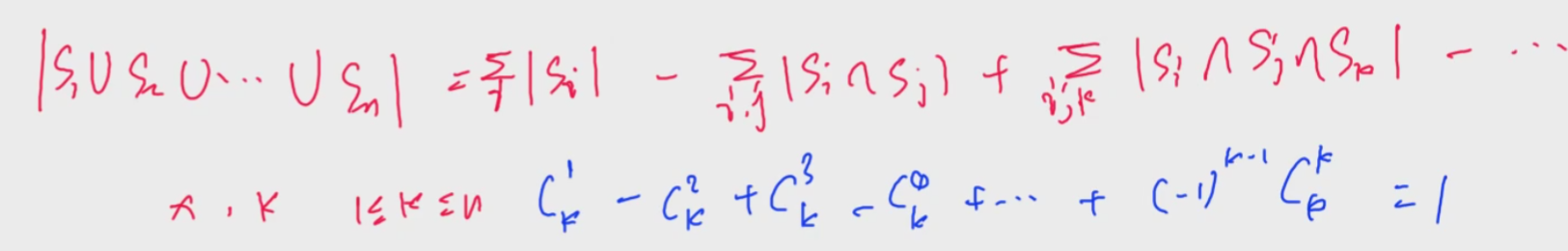coding笔记：Acwing知识点总结
sixwalter Lv6
  2023-08-05 11:14:26 2023-08-05 11:14      25.5k Words  116 Mins  

Acwing 知识点总结

在这个总结里主要讲算法模板和思路，具体的题目代码见刷题.md

第一讲 基础算法

排序

快排

主要思想

快排属于分治算法，分治算法都有三步：

  1. 分成子问题
  2. 递归处理子问题
  3. 子问题合并

寻找一个哨兵，将小于这个哨兵的元素放于其左边，大于他的元素放于其右；递归的排序其左区间和右区间即可完成排序，快排没有子问题合并这一步

think point

  • 如何选取哨兵的位置？

    哨兵的位置应该随机选取，或是取中间：若是取左边作为哨兵，若数组本身就是有序的，每次分划的时间为O(n)，之后的子问题规模即为0和n-1，总共的复杂度即为，而取中间作为哨兵可以保证每次可以把区间分为长度近似相等的两部分，因而复杂度为递归深度*O(n)即为

  • 每次划分两部分后，最终哨兵的位置是否需要获知？

    根据每次分划后是否需要知道哨兵的位置，可以有两种思路来进行快排：

哨兵最终位置未知

第一种思路是acwing的模板思路，缺点是有一些坑，不好理解(i,j位置不能互换，不然可能陷入死循环等)但是代码较为整洁，适合笔试用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void quicksort(int q[], int l, int r) {
    if (l>=r) return;
    // 使用区间中点作为哨兵
    int mid = l+r >>1;
//    swap(q[mid],q[l]);
    int x = q[mid], i = l-1, j= r+1;
    //忽略了哨兵的位置，我不在乎哨兵的位置具体在哪里
    //我只知道，j右边的数都大于等于哨兵，j左边的数都小于等于哨兵
    //之所以不取等于是防止数组越界，还有可以更好地划分子问题
    //缺点是可能会有很多次无效交换
    while(i<j) {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quicksort(q,l,j);
    quicksort(q,j+1,r);
}

算法证明：

明显地，j右边的数大于等于x,i左边的数小于等于x。现需证明while结束时，q[l..j]均<=x，若成立，即可证明j这个端点可以划分整个区间。因为i>=j，所以q[1..j-1]均<=x。因为退出循环前的i<j判断为false，所以最后一次交换不执行，所以q[j]必然<=x。综上可以证明q[l..j]均<=x，所以j这个端点可以划分整个区间。

哨兵最终位置已知

第二种是数据结构教材的官方思路，优点是步骤明确，方便理解，较少坑，缺点是代码冗长

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void quicksort2(int q[], int l, int r) {
    if (l>=r) return;
    // 首先保存哨兵的值
    int pio = q[l];
    int i = l;
    int j = r;
    while(i<j){
        // 之所以可以取=，是因为之前有判断，一定不会越界
        while(i<j && q[j]>=pio) j--;
        if(i<j) q[i] = q[j];
        else break;
        while(i<j && q[i]<=pio) i++;
        if(i<j) q[j] = q[i];
    }
    //哨兵的位置是确定的=i=j，所以只需要对其左边和右边分别进行排序即可
    q[i] = pio;
    quicksort2(q,l,i-1);
    quicksort2(q,i+1,r);
}

算法改进

实际上是对于某类特殊数据的算法增强

如果数组的每个数据都相同时，上面的第一种思路可以pass，但是第二种思路会超过时限，究其原因为：分化后的子问题规模即为0和n-1，总共的复杂度即为，所以对于这种情况需要特殊处理，而且不能简单地将中点与左端点交换（实际上没有改变算法流程），第二种思路地修改点如下：

1
2
3
4
5
6
7
8
while(i<j){
        // 之所以可以取=，是因为之前有判断，一定不会越界
        while(i<j && q[j]>pio) j--;
        if(i<j) q[i++] = q[j];
        else break;
        while(i<j && q[i]<pio) i++;
        if(i<j) q[j--] = q[i];
    }

经测试，第二种思路改进后速度较第一种思路能快上一点点

image-20220509121919959

快排应用—快速选择

主要思想

如果先排序再取第k个数，会导致的复杂度，因此采用快速选择算法，基于快排的模板进行修改即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findKthNumber(int q[],int l,int r,int k){
    if(l==r) return q[l];
    int mid = l+r>>1;
    int x = q[mid];
    int i = l-1,j = r+1;
    while(i<j){
        do{i++;}while(q[i]<x);
        do{j--;}while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    int lol = j-l+1;
    if(k<=lol) return findKthNumber(q,l,j,k);
    else return findKthNumber(q,j+1,r,k-lol);
}
image-20220509174254407
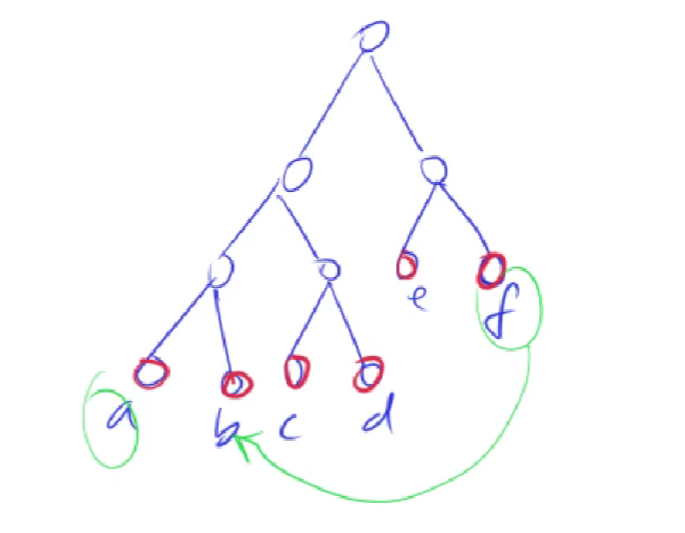
  • 如上图所示，修改点在于如何递归地处理子问题：在（l,r）中寻找第k个数。
  • 而快排给出了找到良好分界点的方式，即j左边的数包括j自身都小于等于x，j右边的数都大于等于x。
  • 因此蓝色区间的数都小于等于红色区间的数，从而如果k小于等于蓝色区间的数的个数，那么第k个数一定在蓝色区间中；反之，如果k大于蓝色区间的数的个数，那么第k个数一定大于等于x,即在红色区间中可以找到。

疑惑与解释

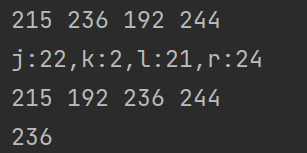
最难理解的地方其实在于边界处，如果k==lol，即第k个数刚好是蓝色区间的个数，我们是否可以直接返回x呢？答案是否定的。原因在于j这个点其实决定了蓝色区间的长度，但是这不代表x就处于j这个位置，即[l..j]可能都小于x，因此第k个数不一定就是x，下图是一个实例，直观解释了这一点：

image-20220509175915922

上图中x是236，j=22指向192这个数，lol=2=k，可见215，192都小于x(236)，236，244都大于等于x，但是返回的却不是第k个数。k=lol只能说明下一步要去寻找蓝色区间里最大的数。

归排

主要思想

首先把待排序数组分成子问题（排序两个长度近似相等的数组），递归处理子问题直到只剩一个元素，两个数组排序完成后需要合并成一个新的排序好的数组，这就是第三步：子问题合并。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int n;
int q[N];
int temp[N];

void mergesort(int q[], int l, int r) {
    if (l >= r) return;
    int mid = l + r >> 1;
    mergesort(q, l, mid), mergesort(q, mid + 1, r);
    int k = l, i = l, j = mid + 1;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j]) temp[k++] = q[i++];
        else temp[k++] = q[j++];
    }
    while (i <= mid) temp[k++] = q[i++];
    while (j <= r) temp[k++] = q[j++];
    for (int i = l; i < r + 1; i++)
        q[i] = temp[i];
}

int main() {
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&q[i]);
    mergesort(q,0,n-1);

    for (int i=0;i<n;i++) printf("%d ",q[i]);
    return 0;
}

归并排序应用—逆序对数量

这个题目相当于套在了归并排序的大框框里。注意合并两个已排序子序列时如何去计算逆序对数量。

二分

整数二分

  • 整数二分因为涉及+1，-1，所以为了防止死循环，需要考虑边界情况。
  • 当我们定义一个性质，该性质可以将数据二分时（即存在边界时），二分算法是可以将该边界找出来的。

主要思想

  • 假设在整个区间内部是可以找到答案的，我们对整个区间不断进行二分
  • 每次都要选择答案所在的区间去进行下一步搜索（每次会把整个区间的大小缩小一半）
  • 二分一定会保证区间里有答案的，但是存在特例，即原问题无解的情况（无解一定和题目有关）
  • 在原问题无解的情况下，若没有遇到数组边界，找到的区间一定是满足条件的，但不是query；而如果遇到数组边界，那么就可能不会满足找到的区间一定是满足条件的（以整数的范围这道题为例）

该图即为寻找满足check的最右端端点示意图

上图对应的代码即为二分模板1的代码，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
bool check(int mid) {return false;}
double function(double){return 0.0;}
// 二分模板1
int bsearch1(int l,int r){
    // 考虑边界，l+1=r时，算法是否正确
    // l+1=r时,需要修改mid=l,会陷入死循环
    // 所以修改mid=(l+r+1)/2,遇到边界时，mid=r,可以顺利退出
    // r会小于l的可能仅在最后一句，但遇到边界且不满足条件时，计算的mid不可能=l,所以退出循环时r不可能小于l,即l=r
    // 返回r,l均可
    while (l<r){
        int mid = l+r+1 >>1;
        // 若check 代表满足条件
        if(check(mid)) l = mid;
        else r = mid-1;
    }
    return l;
}
// 二分模板2
int bsearch2(int l,int r){
    // 寻找不满足的断点
    // 考虑边界，l+1=r时，算法是正确的
    // 退出循环时，l==r的原理同上
    while(l<r){
        int mid = l+r>>1;
        if(check(mid)) l = mid+1;
        else r = mid;
    }
    return l;
}

浮点数二分

  • 较整数二分简单，因为不需要考虑边界（因为没有整除，每次都可以完美地将边界缩小一半）
  • 思想与整数二分一样，只要满足时时刻刻答案都在我们的区间即可；
  • 但我们的区间足够小时，我们就可以认为已经找到了答案；
  • 有两种方式可以去写浮点数二分的循环条件：一个是固定循环100次，如果原来区间长度为1时，结束时区间长度即为；或是指定一个很小的数epsilon，当区间长度小于这个数即可退出。
1
2
3
4
5
6
7
8
9
10
double fbsearch(double l,double r,double target){
    // 浮点数二分查找
    while(r-l>1e-8){
        double mid = (l+r)/2;
        double val = function(mid);
        if (val>=target) r = mid;
        else l = mid;
    }
    return l;
}

应用：数的三次方根

求数的三次方根可以使用二分查找来做。因为函数是单调的，所以很容易判断mid和target的大小关系，从而缩小查找范围，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
double fbiSearch(double l, double r, double target, double (*pf)(double)) {
    while (r - l > 1e-7) {
        double mid = (l + r) / 2;
        if (pf(mid) <= target) l = mid;
        else r = mid;
    }
    return r;
}
double calTrip(double x){
    return x*x*x;
}
int findRoot3(){
    double n;
    double (*pf)(double)=calTrip;
    cin>>n;
    if(n<0) printf("-%.6f",fbiSearch(0,ceil(-n),-n,calTrip));
    else printf("%.6f",fbiSearch(0,ceil(n),n,calTrip));
    return 0;
}

简要介绍下引入的函数指针，有了函数指针就可以方便地将计算方法传入二分查找算法来找解。double (*pf)(double)=calTrip;可以定义一个函数指针，非常有用。

高精度算数

主要思想

  • 如何存储大数？使用数组（vector）

  • 怎么存储？低位在前，高位在后

    之所以这样是因为进位容易，不需要将数组整体向后移动一位

  • 模拟人工算数流程

加法

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> highAccAdd(vector<int>&A,vector<int>&B){
    int c = 0;
    vector<int> C;
    if (A.size()<B.size()) return highAccAdd(B,A);
    for(int i=0;i<A.size();i++){
        if(i<B.size()) c+= B[i];
        c += A[i];
        C.push_back(c%10);
        c /= 10;
    }
    if(c) C.push_back(1);
    return C;
}

减法

  • 减法我们规定只能大数减小数，否则不够借位；
  • 小数减大数可以转化为负的大数减小数
  • (c+10)%10合并了c<0时借位和>0时不用借位的情况；
1
2
3
4
5
6
7
8
bool biggerThan(vector<int>&A,vector<int>&B){
    if(A.size()!=B.size()) return A.size()>B.size();
    else{
        for(int i=A.size()-1;i>=0;i--)
            if(A[i]!=B[i]) return A[i]>B[i];
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> highAccMinus(vector<int>&A,vector<int>&B){
    int c = 0;
    vector<int> C;
    // 我们假设A一定大于B,且均为正数
    for(int i=0;i<A.size();i++){
        c+=A[i];
        if(i<B.size()) c-=B[i];
        C.push_back((c+10)%10);
        if(c<0) c=-1;
        else c=0;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

乘法

  • 高精度乘法实际上是一个大数乘以小数
  • 注意要去除前导零；
1
2
3
4
5
6
7
8
9
10
11
vector<int> highAccMul(vector<int>&A,int b){
    int c = 0;
    vector<int> C;
    for(int i=0;i<A.size()||c;i++){
        if(i<A.size()) c+=A[i]*b;
        C.push_back(c%10);
        c/=10;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

除法

  • 模拟手工除法，注意这次是从高位开始循环，不同于之前的算数
  • 每次的借位可以使用c来存储，使用c*10+A[i]来表示当前的被除数
1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> highAccDiv(vector<int>&A,int b,int*r){
    int c=0;
    vector<int>C;
    for(int i=A.size()-1;i>=0;i--){
        c= c*10+A[i];
        C.push_back(c/b);
        c%=b;
    }
    *r = c;
    reverse(C.begin(),C.end());
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

前缀和和差分

前缀和

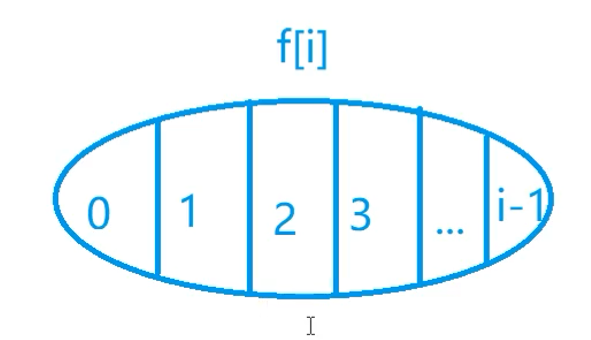
  • 定义：使用s[N]表示数组q[N]的前缀和数组，s[i]表示q[1-i]的元素的和
  • 公式：
  • 注意，下标范围为1-N，且s[0]=0

差分

  • 定义：前缀和的逆运算，假想一个d[N]，使得q[N]是d的前缀和数组，那么d[N]就称为q的差分。
  • 公式：
  • 注意，d下标范围为1-N

前缀和和差分的应用

求一段数的和O(1)

  • 只需要事先处理得到q数组的前缀和s数组，就可以通过在O(1)时间内完成一段数的求和

对一段数加上某个数O(1)

  • 假设我们已经有了差分数组，我们只需要对其求一遍前缀和即可得到原数组，时间复杂度为O(n)
  • 我们对d[i]加上c后，a[i]~最后都会加上c（根据前缀和的定义），所有如果想要给一段数(l,r)都加上c，就只需要d[l]+c，d[r+1]-c

对子矩阵求和O(1)

  • 对一维进行扩展可以得到二维区间和=，图像直观解释如下图：

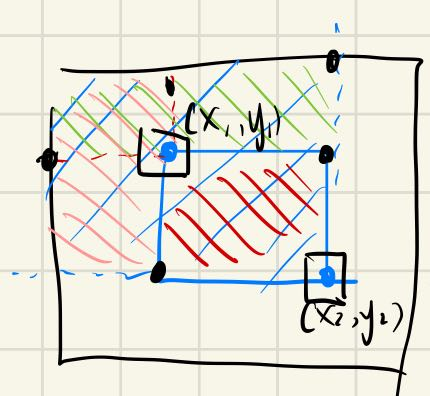
    image-20220606134133525

对二维区间加上某个数O(1)

画图可以清楚的解释该算法：

image-20220606134339757

代码如下：

1
2
3
4
5
6
7
template<int n,int m>
void diffAdd2D(int (&diff) [n][m], int x1,int y1,int x2,int y2,int c){
    diff[x1][y1]+=c;
    diff[x1][y2+1]-=c;
    diff[x2+1][y1]-=c;
    diff[x2+1][y2+1]+=c;
}

注：在代码里我使用了二维数组传参的一种优美方法（使用模板推导出二维数组维度），在函数调用时无须指明维度大小，在函数体内也可以直接索引，从而可以减少代码量。

同理可以进行推广到三维甚至多维数组，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<int n, int m, int q>
void test3Dimens(int (&test)[n][m][q], int x1,int y1,int z1,int c){
    test[x1][y1][z1]-=c;
}

const int Q = 110;
int test3D[Q][Q][Q];

int multiDimenTest(){
    test3D[1][2][3]=6;
    test3Dimens(test3D,1,2,3,6);
    cout<<test3D[1][2][3];
    return 0;
}

推广：3D空间求和O(1)

应该不会考类似的题，但是对于拓展思维应该还是有用的

1
2
3
4
template<int n, int m, int q>
void 3D_Sum(int (&test)[n][m][q], int x1,int y1,int z1,int x2,int y2,int z2){
    return test[x2][y2][z2]-test[x2][y1-1][z2]-test[x1-1][y2][z2]-test[x2][y2][z1-1]+test[x2][y1-1][z1-1]+test[x1-1][y2][z1-1]+test[x1-1][y1-1][z2]-test[x1-1][y1-1][z1-1];
}

双指针算法

指向两个序列

  • 维护某种次序，例如归并排序合并两个有序序列的操作。

指向一个序列（更常见）

  • 两个指针维护的是一段区间，例如快排

代码模板

1
2
3
4
for(i=0,j=0;i<n;i++){
    while(j<i && check(i,j)) j++;
    //每道题的具体处理逻辑
}

核心思想

  • 运用了某些单调的性质，可以把朴素算法O(n2)优化到O(n)

算法应用

  • 把一行字符串中的每个单词分别输出出来，且每个单词占一行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <iostream>
#include <string.h>
int main(){
    char str[1000];
    gets(str);
    int n = strlen(str);
    for(int i=0;i<n;i++){
        int j=i;
        while(j<n && str[j]!=' ') j++;
        for(int k=i;k<j;k++) cout<<str[k];
        cout<<endl;
        i=j;
    }
    return 0;
}
  • 找出最长的不包含重复数字的连续子序列

可以先想暴力的算法，再进行优化

暴力：先枚举终点，再枚举起点 O(n2)

优化：当区间终点向后移动时，区间起点也一定向后移动

可以开一个大数组，动态地确定一下当前区间每个数出现多少次。当加入一个数，如果出现次数>1，则说明重复了，需要更新起点的位置。当数据很大时可以用哈希表来做。

位运算

求整数N其二进制表示中第k位数字是几

个位是第0位，十位是第1位

  • 先把第k位移到最后一位:n>>k
  • 看看个位是几:x&1

lowbit(x)：返回x的最后一位1

公式：x & -x = x & (~x+1)

c++中一个整数的负数是原数的补码，即-x=~x+1

直观解释如下图：

image-20220907161904730

应用：统计整数的二进制表示中1的个数

每一次把它的最后一位1去掉，当x=0时，说明没有1了，减了多少次就说明有多少个1。

离散化

特指整数的离散化，而且是保序的离散化

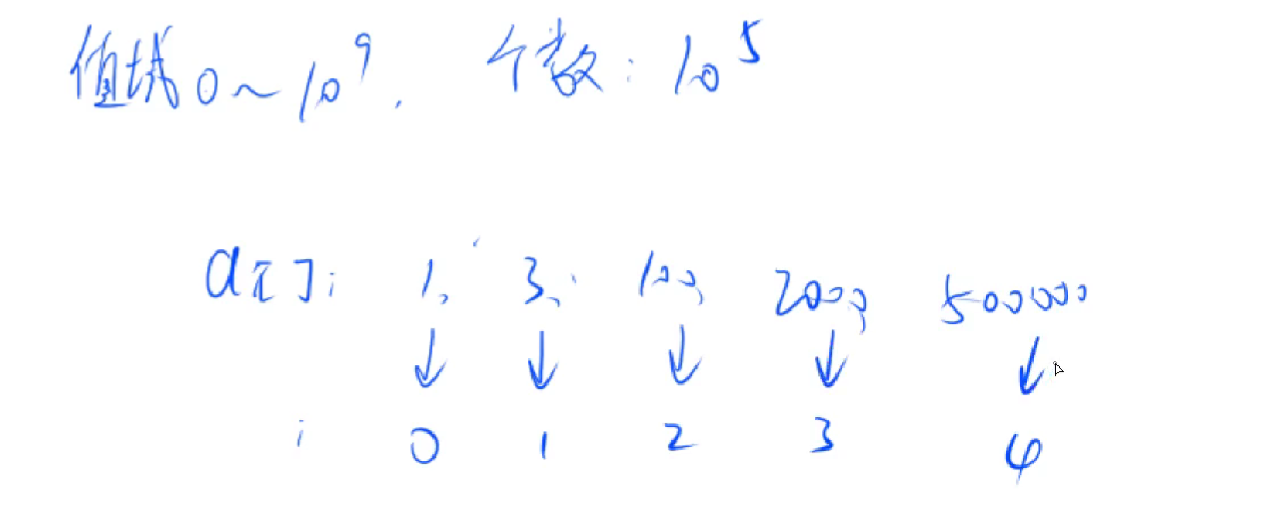
总共的取值范围跨度很大，但是我们只用到了其中的一小部分，非常稀疏。

值域比较大，但是数的个数比较小。过程如图所示：

image-20220907163221798
  • a[]中可能有重复元素，所以需要去重
1
2
3
4
5
//把一个数组排序+去重
vector<int> alls;
sort(alls.begin(),alls.end());
// unique将所有元素去重，并且范围去重后元素的尾端点
alls.erase(unique(alls.begin(),alls.end()),alls.end());
  • 如何算出a[i]离散化后的值？

通过二分求出离散化后的值：找到第一个大于等于x的位置

1
2
3
4
5
6
7
8
9
int find(int x){
    int l=0,r=alls.size()-1;
    while(l<r){
        int mid = l+r>>1;
        if(alls[mid]>=x) r = mid;
        else l = mid+1;
    }
    return r+1;//映射到1,2,...,n
}

应用：求区间所有数的和

结合前缀和和离散化，将每一个可能用到的下标存到vector alls中，操作的新下标即离散后化的值，每个操作在新数组上进行

区间合并

将所有有交集的区间进行合并，输出合并后的区间个数

贪心的思想

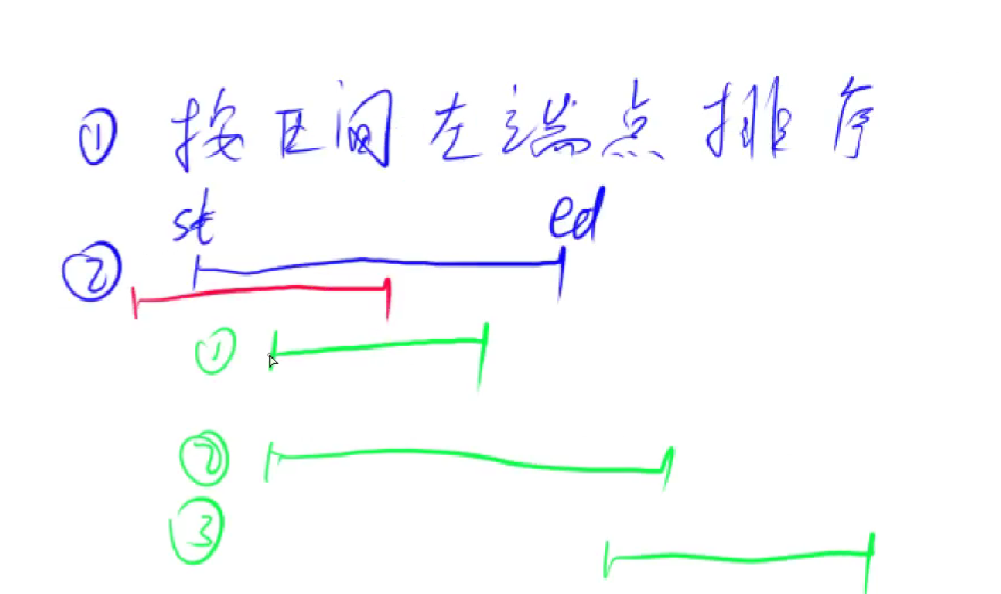
按照区间的左端点排序，扫描所有区间，当前区间和前面维护的区间的位置关系如下图：

image-20220907171913269

可以使用pair来存储区间端点，使用vector来存储所有区间。使用st,ed表示当前维护区间的端点，若遍历区间与维护区间没有交集，就可以将维护区间加入result数组中去，否则更新维护区间的端点。

第二讲 数据结构

这里默认已经对基本的数据结构有所了解，因此重点在于数组模拟练习与总结。对于算法题而讲，使用数据模拟的好处不言而喻（速度快），是STL外的一大解题利器。

变量和代码解释都写在了注释里，可以方便之后的回顾。p.s. 为了方便，有的简单的注释就直接用英语打了，可以减少输入法的繁琐切换。

链表

单链表

  • 数据准备及初始化
1
2
3
4
5
6
7
8
9
10
11
//单链表
const int N = 100010 //就实际工程而言，定死可能不太优美，注意优化方案
int e[N];// store the value of the nodes
int ne[N];// store the ptrs of next node 
int head;// store the index of head node
int idx;// store the current available index

void init(){
    head = -1;//注意：一开始链表为空，使用-1来辨识空结点
    idx = 0;
}
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//insert to the head of the list
void add_to_head(int x){
    e[idx] = x;
    ne[idx] = head;
    head = idx++;
}
//insert the node after the k(index) node
void insert_k(int k, int x){
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}
//remove the node after the k(index) node
void remove_k(int k){
    ne[k] = ne[ne[k]];
}
  • 应用：删除倒数第二个结点 O(n)

用一个额外的pre来保存当前遍历结点的前两个结点，只要当前结点的下一结点非空就一直遍历，否则退出循环，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void remove_l2(){
    int pre = -1;
    int cnt=0;
    int cu = head;
    while(ne[cu]!=-1){
        cnt++;
        if(cnt>1){
            if(pre==-1) pre = head;
            else pre = ne[pre];
        }
        cu = ne[cu];
	}
    remove_k(pre);
}

双链表

  • 数据准备与初始化
1
2
3
4
5
6
7
8
9
int e[N];
int l[N]; //store the pre idex of current node
int r[N]; //store the next idex of current node
int idx; // store the current available node
void init(){
    r[0]=1; // 默认0号点为左边界，1号点为右边界
    l[1]=0;
    idx = 2;
}
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// insert a node at the head of the list
void insert_left(int x){
    insert_k_right(0,x);
}
//insert a node at the end of the list
void insert_right(int x){
    insert_k_left(1,x);
}
//insert a node to the k(index) node 's left
void insert_k_left(int k, int x){
    insert_k_right(l[k],x);
}
//insert a node to the k(index) node 's right
void insert_k_right(int k, int x){
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]]=idx;
    r[k] = idx++;
}
// delete the k(index) node 
void delete_k(int k){
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

栈

先进后出

  • 数据准备与初始化
1
2
int stk[N];
int tt=0;
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//push to the top of stack
void push(int x){
    stk[++tt]=x;
}
//pop the top of the stack
void pop(){
    if(tt>0) tt--;
}
//check if the stack is empty
bool isEmpty(){
    if(tt) return false;
    else return true;
}
//query the top of the stack
int top(){
    return stk[tt];
}

一种可能的优化：面向对象的封装+任意类型的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
const int N = 100010;

template<class T>
class Stack {
    T stk[N];
    int tt;
public:
    Stack(){
        init();
    }

    //init
    void init() { tt = 0; }

    // pop
    T pop() { return stk[tt--]; }

    // push
    void push(T x) { stk[++tt] = x; }

    // isempty
    bool isEmpty() {
        if (tt > 0) return false;
        else return true;
    }
    void printStack(){
        printf("--------------\n");
        for(int i =1;i<=tt;i++) printf("%c ",stk[i]);
        printf("--------------\n");
    }

    // top
    T queryTop() { return stk[tt]; }
};

队列

先进先出

  • 数据准备与初始化
1
2
3
4
5
6
7
int q[N];
int hh,tt;//指向队头和队尾元素

void init(){
    hh=0;
    tt=-1;
}
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//向队尾插入一个数
void push(int x){
    q[++tt] = x;
}
//从队头弹出一个数
int pop(){
    if(!isEmpty()) return q[hh++];
    else printf("error");
}
//判断队列是否为空
bool isEmpty(){
    if(hh>tt) return true;
    else return false;
}
//查询队头元素
int top(){
    if(!isEmpty()) return q[hh];
    else printf("error");
}

单调栈和单调队列

主要思路

  • 先想一个朴素做法
  • 再想队列或栈中哪些元素是没有用的，然后把所有这些没有用的元素删掉
  • 再看一下有没有单调性，怎么去优化这个问题

应用场景

  • 单调栈：给定一个序列，求序列中的每一个数左边离它最近的，且比它小的数在什么地方
image-20220909170603704

主要思想即，比当前遍历元素大的栈中的数永远不会再用到。每个元素进栈一次，最多出栈一次，因此时间复杂度为O(N)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//暴力做法
for(int i=0;i<n;i++)
    for(j=i-1;j>=0;j--)
        if(a[i]>a[j]){
            cout<<a[j]<<endl;
            break;
        }
#include<stack>
//单调栈做法
int main(){
    int n;
    cin>>n;
    stack<int> st;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        while(st.size() && x <= st.top()){
            st.pop();
        }
        if(!st.size())
            cout<<-1<<' ';
        else
            cout<<st.top()<<' ';
        st.push(x);
    }
}
  • 单调队列：求一个滑动窗口里的最大值或最小值
image-20220913153009278

主要思想是使用一个队列来维护窗口里的所有数（下标），只有前面一个数比后面的一个数大，我们就可以断定，前面的点一定没有用，因此可以把这个点删掉。只要有逆序对，我们就可以把大的点删掉，把所有这些点删掉的话，整个数列就会变为一个严格单调上升的队列，其最小值正是队头。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//暴力做法:O(Nk)
//遍历队列中的所有数

//优化
#include<queue>
using namespace std;
const int N = 1000010;
int a[N];
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    queue<int> que;
    for(int i=0;i<n;i++){
        int head = que.front();
        if(que.size()&&i-k==head) que.pop();
        while(que.size&&a[que.back()]>= a[i]) que.pop_back();
        que.push(i);
        if(i>=k-1) printf("%d ",que.front());
    }
}

Trie

  • 概念：用于高效存储和查找字符串集合的数据结构

  • 数据准备与初始化

1
2
3
4
5
6
7
int son[N][26]; //假设只有大写字母A-Z,存储当前结点的所有子结点
int cnt[N]; //记录以i为结尾的字符串的个数
int idx; //存储当前可用的索引
//下标为0的点既是根结点又是空结点
void init(){
    idx = 1;
}
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
char str[N];
// add a string to the trie
void insert(char str[]){
    if(!str[0]) return;
    int cu = 0;
    for(int i=0;str[i];i++){
        int k = str[i]-'A';
        if(!son[cu][k]) son[cu][k] = idx++;
        cu = son[cu][k];
    }
    cnt[cu]++;
}
// query the number of occurances of the string in the trie
int find_occur(char str []){
    if(!str[0]) return 0;
    int cu = 0;
    for(int i=0;str[i];i++){
        int k = str[i]-'A';
        if(!son[cu][k]) return 0;
        cu = son[cu][k];
    }
    return cnt[cu];
}

并查集

  • 概念：可以快速处理并维护

    • 将两个集合合并
    • 询问两个元素是否在一个集合中

  • 如果使用暴力解法，合并两个集合需要O(n)的时间，而并查集可以在O(1)的时间内近似完成这两个操作。

  • 数据准备与初始化

1
2
3
4
5
6
7
int fa[N]; // store the parent index of each node
// only the root node has the property of fa[root]=root'
void init(){
    int num;
    cin>>num;
    for(int i=1;i<=num;i++) fa[i]=i;
}
  • 数据操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// find the set(root) index which num x is in
int find_root(int x){
    //if current node is not root
    if(fa[x]!=x) fa[x]=find_root(fa[x]); // path compression
    return x;
}
// combine two sets which num a/b is in
void combine(int a, int b){
    int r_a = find_root(a);
    int r_b = find_root(b);
    if(r_a != r_b) fa[a]= b;
}
// query whether two num are in the same set
bool inSameSet(int a, int b){
    return find_root(a)==find_root(b);
}

堆

  • 在STL中也称为优先队列priority queue

  • 数据准备与初始化

1
2
3
4
5
6
int heap[N];//heap is a 完全二叉树
int size;
int cnt; // cnt the num of insert
int cti[N],itc[N]; // preserve a count to index mapping and a index to count mapping
// cause 2*i is the left node index and 2*i+1 is the right node index
// so we have to start at the index 1
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// swap
void myswap(int x, int y){
    swap(heap[x],heap[y]);
    swap(cti[itc[x]],cti[itc[y]]);
    swap(itc[x],itc[y]);
}
// build a heap
void buildHeap(){
    for(int i = size/2;i;i--){
        down(i);
    }
}
// up
void up(int x){
    if(x/2 && heap[x/2]>heap[x]){
        myswap(x/2,x);
        up(x/2);
    }
}
// down
void down(int x){
    int min_i = x;
    if(2*x<=size && heap[min_i]>heap[2*x]) min_i = 2*x;
    if(2*x+1<=size && heap[min_i]>heap[2*x+1]) min_i = 2*x + 1;
    if(min_i!=x) {
        myswap(min_i,x);
        down(min_i);
    }
}
// insert a num
void insert(int num){
    heap[++size] = num;
    itc[size] = ++cnt;
    cti[cnt] = size;
    up(size);
}
// output the min num of the heap
int min_val(){
    return heap[1];
}
// delete the min num of the heap
void delete_min(){
    myswap(1,size--);
    down(1);
}
// delete the kth insert num
void delete_k(int k){
    // put the num at position size of the heap(end) to the position cti[k]
    // if we don't know the itc(index to count mapping)
    // we can't update the new cti[itc[size]] which is actually cti[k]
    // so we need a two way mapping
    int tmp = cti[k]; // store this value because the function below it may change its value
    myswap(tmp, size--);
    up(tmp),down(tmp);
}
// modify the kth insert num to x
void modify_k(int k, int x){
    heap[cti[k]] = x;
    up(cti[k]),down(cti[k]);
}

哈希表

存储结构

开放寻址法

以开放寻址为主例，因为开的空间小，且写起来简单；拉链法仅贴出代码

  • 数据准备与初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int h[N];
//列表长度取>操作集合2倍大小的最小质数，不容易起冲突
int null = 0x3f3f3f3f;// 该数大于10^9，一般看作最大整型，这里取不可能出现的数作为空值

// 使用下面的函数即可得到N的大小为200003
void find_min_prime(int x){
    for(int i=x;;i++){
        bool flag = true;
        for(int j=2;j*j<i;j++){
            if(i%j==0) {
                flag=false;
                break;
            }
        }
        if(flag) {
            printf("%d",i);
            break;
        }
    }
}
void init(){
    memset(h,0x3f,sizeof h);//将所有entry置为null
}
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// find the index where the num should be(exists if h[index] not null) 
int find(int x){
    int k = (x%N+N)%N; // not to make it negative, compute the hash Which is often the mod operation. 
    while(h[k]!=null && h[k]!=x){
        k++;
        if(k==N) k=0;
    }
    return k;
}
// query whether the num is in the hash table
bool hasNum(int x){
    if(h[find(x)]!=null) return true;
    else return false;
}
// insert a num into hash table
void insert(int x){
    if(!hasNum(x)) h[find(x)]= x;   
}

拉链法

  • 数据准备与初始化
1
2
3
int h[N] // N = 100003 
int e[N],ne[N],idx;
memset(h,-1,sizeof h);//-1代表为空
  • 数据操纵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//拉链法
// insert a num into hash table, can be duplicate in this situation
int insert(int x){
    int k = (x%N+N)%N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k]= idx++;
}
// query whether the num is in the hash table
bool hasNum(int x){
    int k = (x%N+N)%N;
    int cu = h[k];
    while(cu!=-1) {
        if(e[cu]==x) return true;
        cu = ne[cu];
    }
    return false;
}

字符串哈希

字符串前缀哈希法

首先，要预处理出所有前缀的哈希：

image-20220908153513235

note: h[1]=前缀的哈希值

如何求字符串哈希值？

image-20220908153854968
  • 把字符串看作一个P进制的数
  • 把P进制数转换为10进制数
  • 取模，就可以把任何一个字符串映射为0~Q-1之间的数

注意：

  • 不要把某个字母映射成0

  • 假定我们rp足够好，不存在冲突

  • p=131或13331，Q=2^64时，99.9%都不会出现冲突

  • 预处理前缀哈希：h(i) = h(i-1)*p + str(i)

  • 利用前缀哈希可以求出所有子串的哈希值: h(R) -h[L-1]*p^(R-L+1)

  • 另外用unsigned long long来存Q，即可以省略取模这步（因为会溢出）

字符串哈希的作用？

除了不能求循环节，其他好像都代替KMP

快速判断两个字符串是否相同：O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
typedef unsigned long long ULL;

const int N = 100010, P=131;

int n,m;
char str[N];
ULL h[N],p[N];

ULL get(int l, int r){
    return h[r]-h[l-1]*p[r-l+1];
}
int main(){
    scanf("%d%d%s",&n,&m,str+1);
    p[0]=1;
    for(int i=1;i<=n;i++){
        p[i] = p[i-1]*P;
        h[i] = h[i-1]*P+str[i];
    }
    while(m--){
        int l1,r1,l2,r2;
        scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
        
        if(get(l1,r1)==get(l2,r2)) puts("Yes");
        else puts("No");
    }
    return 0;
    
}

STL

vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<int> a;
a.size();
a.empty();
a.clear();//清空
a.front()/back();
a.push_back()/pop_back();
a.begin()/end();//end为最后一个数的后面一个数
//系统为某一程序分配空间时，所需时间与空间大小无关，但与申请次数有关
//所以vector通过倍增尽可能减少申请次数

//遍历
for(vector<int>::interator i = a.begin();i!=a.end();i++) cout<<*i<<' ';
//前面一大串类型可以直接写为auto，比较省事
//范围遍历
for(auto x:a) cout<<x<<' ';

//比较运算
//a<b(字典序)

pair

1
2
3
pair<int,string>p;
//支持比较运算,字典序
p={20,"abc"};

string

1
2
3
4
5
6
7
string a = "sdf";
a+="uyiu";

a.substr(1,2);//从1开始，长度为2的子串

//c_str()：返回string对应的字符数组的头指针
printf("%s\n",a.c_str());

queue

1
2
3
4
5
//从队尾插入，从队头删除
push()
front()
back()
pop()

priority_queue

1
2
3
4
5
6
7
priority_queue<int> heap;
//定义小根堆
priority_queue<int,vector<int>,greater<int>> heap;
push()
top() //返回堆顶元素
pop();

stack

1
2
3
push()
top()
pop()

deque

双端队列，加强版vector，但速度慢

1
2
3
4
5
#include<deque>
front()/back();
push_back()/pop_back();
push_front()/pop_front();
begin()/end()

set

基于平衡二叉树，本质上动态维护一个有序序列，支持begin()/end()

1
2
3
4
5
6
7
8
9
10
11
set<int>s;//不能有重复元素
s.insert(); //插入一个数log(n)
s.find();
s.count();//返回某个数的个数
s.erase();
// 输入是一个数x，删除所有x的复杂度为O(k+log(n))
// 输入是一个迭代器，删除这个迭代器
s.lower_bound()/upper_bound();
// lower_bound返回大于等于x的最小的数的迭代器
// upper_bound返回大于x最小的数的迭代器
multiset<int>ms;//可以有重复元素

map

基于平衡二叉树，本质上动态维护一个有序序列

1
2
3
4
5
6
7
8
insert();//插入的是一个pair
erase();//输入是pair或迭代器
find();
[]//时间复杂度是log(n)

map<string, int> a;
a["hht"] = 1;
cout<<a["hht"]<<endl;

unordered_set

哈希表，绝大部分操作时间复杂度为O(1)

1
//凡是和排序有关的操作都是不支持的

bitset

压位：若需要开一个空间为10000*10000 bool数组 10^8B=100mb 若题目很不巧，空间为64mb，我们就可以用bitset来存，可以节省8位空间。

1
2
3
4
5
6
7
8
9
10
bitset<10000> s;
~,&,|,^
<<,>>
count()返回有多少个1
any()判断是否至少有一个1
none判断是否全为0
set()把所有位，置为1
set(k,v)把第k位变成v
reset()把所有位，置为0
flip(k)把第k位取反

KMP

KMP算法在各种参考书中均有讲解，但均较为复杂，且不易于理解其中原理，现佐以笔记，记录自己的学习心得

因为kmp算法相对抽象，因此本文大多辅以图像方便理解

参考视频：https://www.bilibili.com/video/BV1MY4y1Y7Nh

问题描述

给定一个模式串 S，以及一个模板串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串 P 在模式串 S 中多次作为子串出现。

求出模板串 P 在模式串 S 中所有出现的位置的起始下标。

输入格式

第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式

共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围

1≤N≤10^5
1≤M≤10^6

核心思想

  • 先想暴力枚举怎么做的
1
2
3
4
5
6
7
8
9
10
for(int i=1;i<=n;i++){
    bool flag = true;
    int t_i = i;
    for(int j=1;j<=m;j++,t_i++){
        if(S[t_i]!=P[j]){
            flag = false;
            break;
        }
    }
}

复杂度：O(nm)，浪费了额外信息

  • 如何去优化的
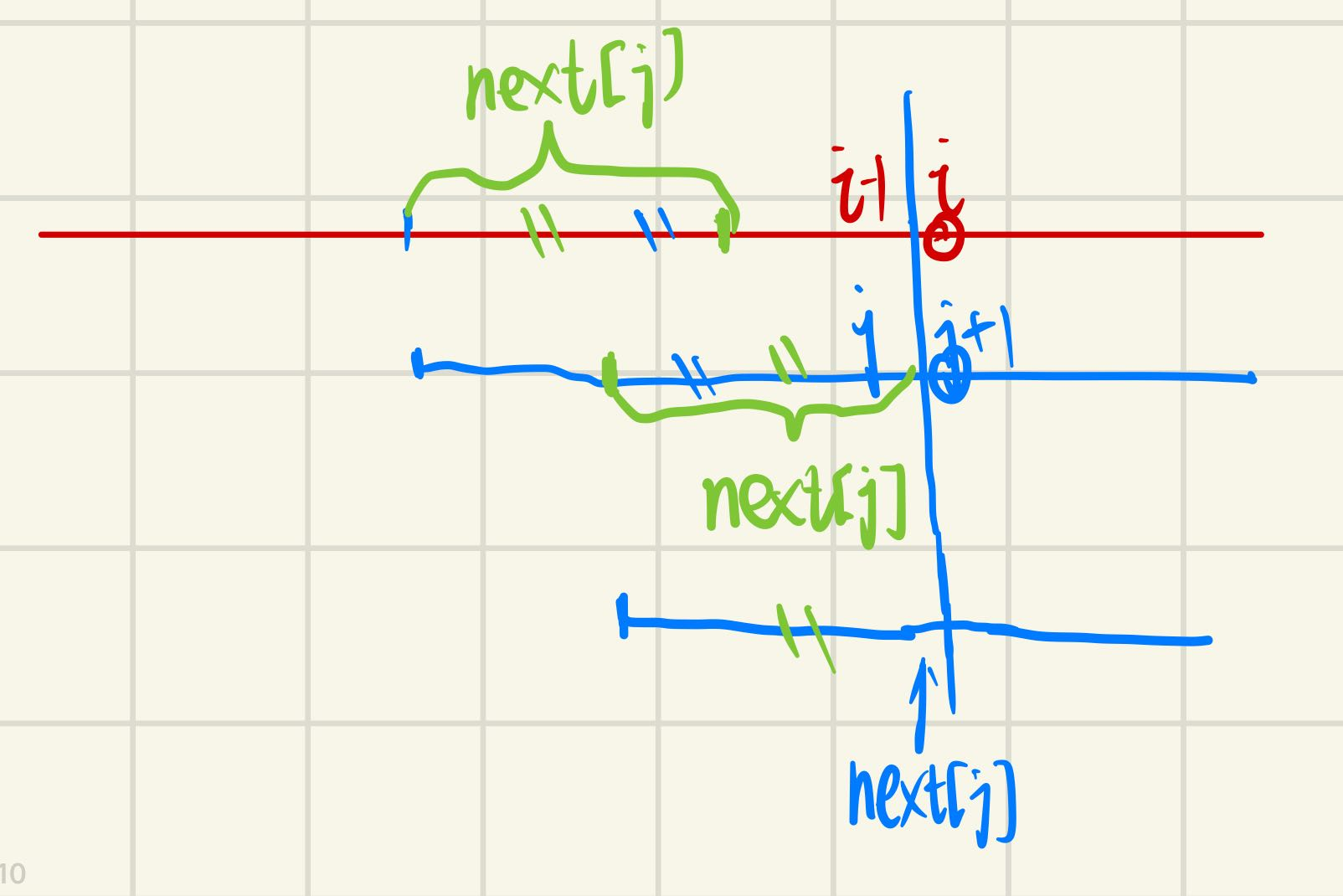
image-20220526112430740

如图，假设现在已匹配了j个字符，但是第j+1个字符不匹配，即，这里S为红色的目标串，P为蓝色的模式串。不匹配时，需将模式传尽可能少的往后移动（我的理解是为了防止漏掉正解），使得移动后的模式串仍与目标串匹配且长度为next[j]，这里采用的思想是不浪费过去已匹配的信息的同时确保找到所有的解，这里只需简单的令即可减少无用的重复匹配次数，然后再判断P[next[j]+1]和S[i]是否相等，不相等则重复上述步骤直到j=0。

最大前后缀相等长度

上述的next[j] = u 的定义为：**P[1,j]的前缀和后缀相等的最大长度(不包括本身)**，之所有取最大前文也有解释，是为了确保找到所有解。

next数组求解

既然问题的关键在于求解next数组，那么找到行之有效的算法是很必要的。这里的思想为归纳法：假设我们已经求解出了next[1,i-1]，现在求出next[i]即可归纳求出整个next数组。依旧可以看上面的图，因为next[i-1]已知，我们可以把模式串移到对应的位置，判断P[i]是否等于P[next[i-1]+1]。若相等说明next[i] = next[i-1] + 1；若不等令P[next[next[i-1]]+1]和P[i]再进行判断，若一直不满足，那么直到next[…] = 0，说明P[1,i]的前缀和后缀相等的最大长度为0，因此next[i]则为0。

next[i] = next[i-1] + 1

下面用反证法解释下为什么该式是成立的：若存在一个更长的前缀和后缀相等的子串，那么同时去掉一个刚匹配的字符，则剩下的串比next[i-1]也要长，这与假设next[i-1]已经是最长的相互矛盾，因此next[i]所存的就是P[1,i]的前缀和后缀相等的最大长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 求解next数组
// 注：next[1]=0如果第一个字符匹配失败了
for(int i=2,j=0;i<=n;i++){
    while(j && P[j+1]!=P[i]) j = ne[j];
    if(P[j+1]==P[i]) j++;
    ne[i] = j;
}

// kmp匹配
for(int i=1,j=0;i<=m;i++){
    while(j && P[j+1]!=S[i]) j = ne[j];
    if(P[j+1]==S[i]) j++;
    if(j==n){
        print("%d ", i-n);
        j = ne[j];
    }
}

KMP算法应用

字符串的循环节

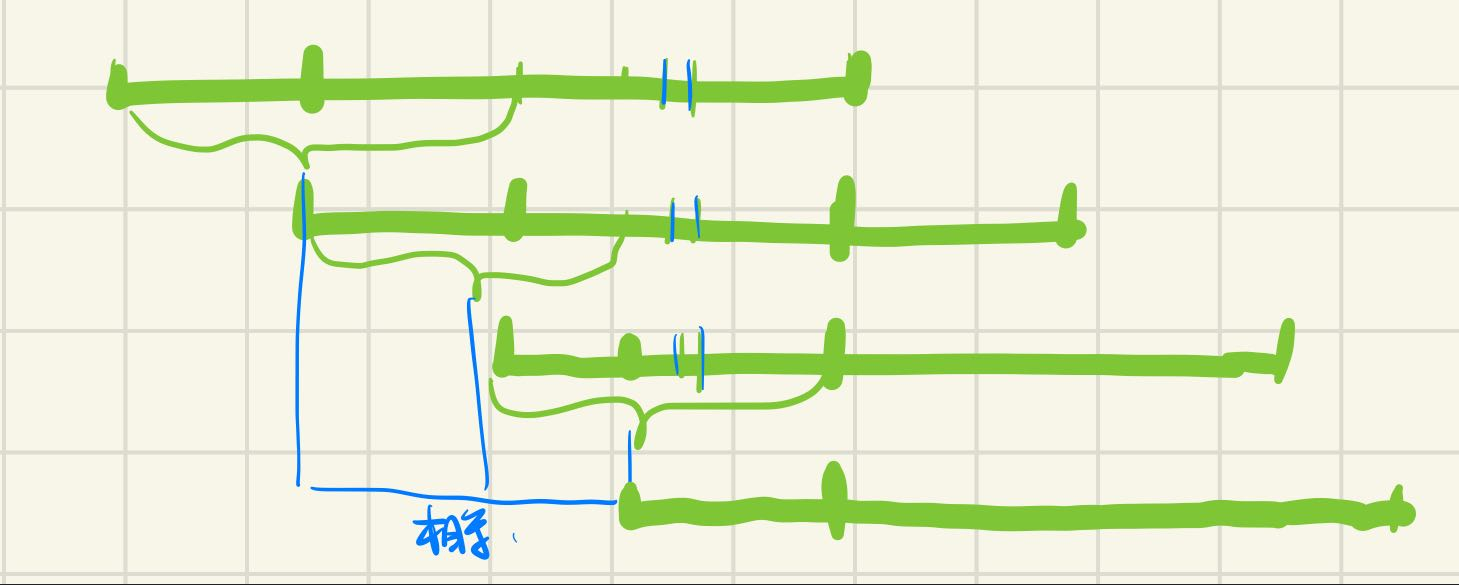
next数组的解法可以让我们求出字符串的循环节：n-next[n]

image-20220526121842989

由图，因为绿色字符串的前缀和后缀相等的最大长度为next[n]，因此我们可以将该串向后移动n-next[n]，使得重叠部分恰好相等。又因为下面的串是平移的，因此上面串的第一段就等于下面串的第一段且长度为n-next[n]，又下面串的第一段与上面串的重叠部分相等（第二段），因此上面串的第一段和第二段相等，以此类推上面串的所有段都相等且以n-next[n]为长度进行循环，因此是字符串的循环节。

  • 不具有循环节的串

例如，“abcdefgh”,不重复的串是不可能有循环节的，若是以其作为模式串，next[i]均为0，kmp算法最多比较O(m+n)次

  • 循环节最多的串

例如，“aaaaaaa”，每个字符都相等的串的循环次数最多，若是以其为模式串，kmp算法最多比较匹配O(2m)次

详细证明可参考博客

字符串所有前后缀相等的子串

image-20220526125319859

这个求解实际和循环节的求解是完全相似的。每次我们将字符串向后平移(实际上是令j = next[j])，求出next数组后我们可以很方便的求出其所有前缀与后缀相等的子串P[:next[j]], j = next[j] util j = 0

现证明该算法为什么能找到所有前后缀相等的子串

假设存在长度为k的前后缀未能通过上述递归式找到。我们先去找长度大于k的长度为i_t的前后缀，假设找到了且为图中第一段的next[n]，那么下一段next[next[n]]即是以next[n]为结尾的最长的前后缀，因为k也是前后缀，但是k比next[next[n]]长与next[next[n]]的定义相互矛盾，所以k必然不存在，因此算法找到了所有前后缀相等的子串。

第三讲 搜索

DFS

执着的算法

  • 思想

    会尽可能往深了搜，搜不到了就回溯，每一次回溯完之后判断当前是不是所有的路径均已遍历，若均已遍历，再进行回溯，否则搜索未遍历的路径

  • 两个重要概念

    • 回溯

      注意恢复现场

    • 剪枝

      最优性剪枝：当前的路径判断一定不如最优解，就可以剪枝了

      可行性剪枝：提前判断当前方案一定是不合法的，那么下面的子树就可以不用进行搜索了

  • 顺序：重要的是顺序，即我们要用一个什么样的顺序将某一道题的所有方案全部遍历一遍

  • 举例：

全排列问题—最经典DFS的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int N = 10;
int path[N];
bool st[N];
//求1-n的全排列数量
void dfs(int h,int n){
    if(h==n){
        for(int i=0;i<n;i++)
            printf("%d ",path[i]);
        puts("");
    }
    for(int i=1;i<=n;i++){
        if(!st[i]){
            path[h] = i;
            st[i] = true;
            dfs(i,h+1,n);
            st[i] = false;
        }
    }
}

n-皇后问题

  1. 第一种搜索顺序：按全排列思路枚举8皇后问题。枚举每一行这个皇后应该放到哪一列上去（经过了某种程度的优化，因为两个皇后不可能在同一行），与全排列的搜索顺序完全一致，同一对角线上的元素必定满足上图的直线方程，所以可以用截距b作为直线的编号。我们可以用剪枝的思想来优化算法，即提前判断当前方案肯定是不合法的，就没必要搜索下去了。O(n*n!)
image-20220610145412486 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
const int N = 20;
bool col[N];
bool diag[2*N],udiag[2*N];
char Q[N][N];
// 无需对queencnt计数，比视频里的方法快了4，5ms
void initBoard(int n){
    for(int i = 1;i<=n;i++) {
        for (int j = 1; j <=n; j++)
            Q[i][j] = '.';
    }
}
void nqueen_dfs(int r,int n){
    for(int i=1;i<=n;i++){
        if(!col[i]&&!diag[i+r]&&!udiag[i-r+n]){
            
            col[i] = diag[i+r]= udiag[i-r+n] = true;
            Q[r][i] = 'Q';
            
            if(r==n){
                for(int k=1;k<=n;k++){
                    for(int j=1;j<=n;j++){
                        printf("%c",Q[k][j]);
                    }
                    puts("");
                }
                puts("");
                Q[r][i] = '.';
                col[i] = diag[i+r]= udiag[i-r+n] = false;
                return;
            }
            
            nqueen_dfs(r+1,n);
            Q[r][i] = '.';
            col[i] = diag[i+r]= udiag[i-r+n] = false;
        }
    }
}
  1. 第二种搜索顺序： 更加原始的一种搜索方式，对于每一个格子，选择是否放皇后， 挨个枚举所有格子，当枚举到最后一个格子(N^2)的时候即得到答案。O()

对于这种思路我们应该如何处理呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//挨个枚举所有格子，放是一个分支，不放是另一个分支  
void dfs(int x, int y, int s){
    if(y==n) y=0,x++;
    if(x==n){
        if(s==n){
            for(int i=0;i<n;i++) puts(g[i]);
            puts("");
        }
    }
    // 不放皇后
    dfs(x,y+1,s);
    // 放皇后
    if(!row[x] && !col[y] && !dg[x+y] && !udg[x-y+n]){
        g[x][y]='Q';
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = true;
        dfs(x,y+1,s+1);
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = false;
        g[x][y]='.';
    }
    
}

BFS

稳重的算法

  • 思想

    每次扩展一层，只有当前层全搜索过了之后，才会去搜索下一层，第一次搜到的话一定是最短的

DFS和BFS对比

搜索方式 占用空间 数据结构 最短路性质 应用场景
DFS O(h) stack 不可以搜到最短路 对空间要求高的
BFS O(2^h) queue 可以搜到最短路（边权重为1时） 最小步数，最短距离，最少操作次数
  • 举例：

走迷宫—最短路问题；dp问题实际上是没有环的最短路

  • 基本框架
    • 将初始状态放入队列
    • 只有队列不空便循环:
      • 每次把队头拿出来
      • 扩展队头
image-20220909163046195 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//迷宫问题--如何将框架应用起来
#include<queue>
//数据准备与初始化
int g[N][N]; // store the map
int d[N][N]; // store the distance to the start entry,初始化为-1代表没访问过
int dir[5]={-1,0,1,0,-1}
int bfs(){
    queue<int> que;
    que.push({0,0});
    memset(d,-1,sizeof d);
    d[0][0]=0;
    while(que.size()){
        auto cu = que.front();
        for(int i=0;i<4;i++){
            int x = cu.first +dir[i];
            int y = cu.second+dir[i+1];
            if(x<n && x>=0 && y<m && y>=0 && d[x][y]==-1 && g[x][y]==0){
                d[x][y] = d[cu.first][cu.second]+1;
                que.push({x,y});
            }
        }
        
    }
    return d[n-1][m-1];
}
int main(){
    cin>>n>>m;
    
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin>>g[i][j];
    cout<<bfs()<<endl;
    return 0;
}

第四讲 图论

树是一种特殊的图，即树是无环连通图，所以只讲图这个更广泛的数据结构就可以了

树和图的存储

无向图

边是无方向的，对于每一个无向边，可以建两条边：建一条由a到b的，再建一条由b到a的，因此无向图是一种特殊的有向图，我们只需考虑有向图就可以了

有向图

有向图有度数的概念：入度和出度

  • 邻接矩阵

开个二维数组即可，适合存储稠密图（浪费空间）

  • 邻接表

n个点每个点都有一个单链表，存储从该点可以到的所有的点

考虑最坏情况需要开的数组大小（来存单链表），如果是完全无向无图（n个点），每个点都可以到达其他所有点（n-1个边），所以总共要开的大小

插入一条新的边（头插法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<iostream>
using namespace std;
const int N = 100010,M = N*2;// 如果是树的话可以这么做
int h[N],e[M],ne[M],idx;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
} 

void init(){
    memset(h,-1,sizeof h);
}

树和图的遍历

深度搜索

1
2
3
4
5
6
7
8
9
bool st[N];//存储哪些点已经被遍历过了
// u 表示当前已经遍历到的点
void dfs(int u){
    st[u] = true;//标记一下，这个点已经被搜过了
    for(int i=h[u];i!=-1;i=ne[i]){
        int j = e[i];// 找到i这个索引所对应的图的结点的编号是多少
        if(!st[j]) dfs(j);
    }
}
  • 实例：树的重心

宽度搜索

求从1号点到n号点的最短路，如果无解，输出-1：

image-20220914143716317 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int bfs(){
    int hh=0,tt=0;
    q[0]=1;
    memset(d,-1,sizeof d);
    d[1]=0;
    while(hh<=tt){
        int t = q[hh++];
        for(int i=h[t];i!=-1;i=ne[i]){
            int j = e[i];
            if(d[j]==-1){
                d[j] = d[t] + 1;
                q[++tt] = j;
            }
        }
    }
    return d[n];
}
  • 实例：求拓扑序

有向无环图才会有拓扑序列，所以也被称为拓扑图，且不一定是唯一的

求解思路

所有入度为0的点都可以排在当前最前面的位置；

枚举t的所有出边t->j，删掉t->j，入度d[j]–，如果d[j]==0，就让j入队。

最短路

难点在于建图，而不在算法的原理上：给你一个背景，如何把问题抽象成最短路，侧重于实现思路，而不侧重于原理

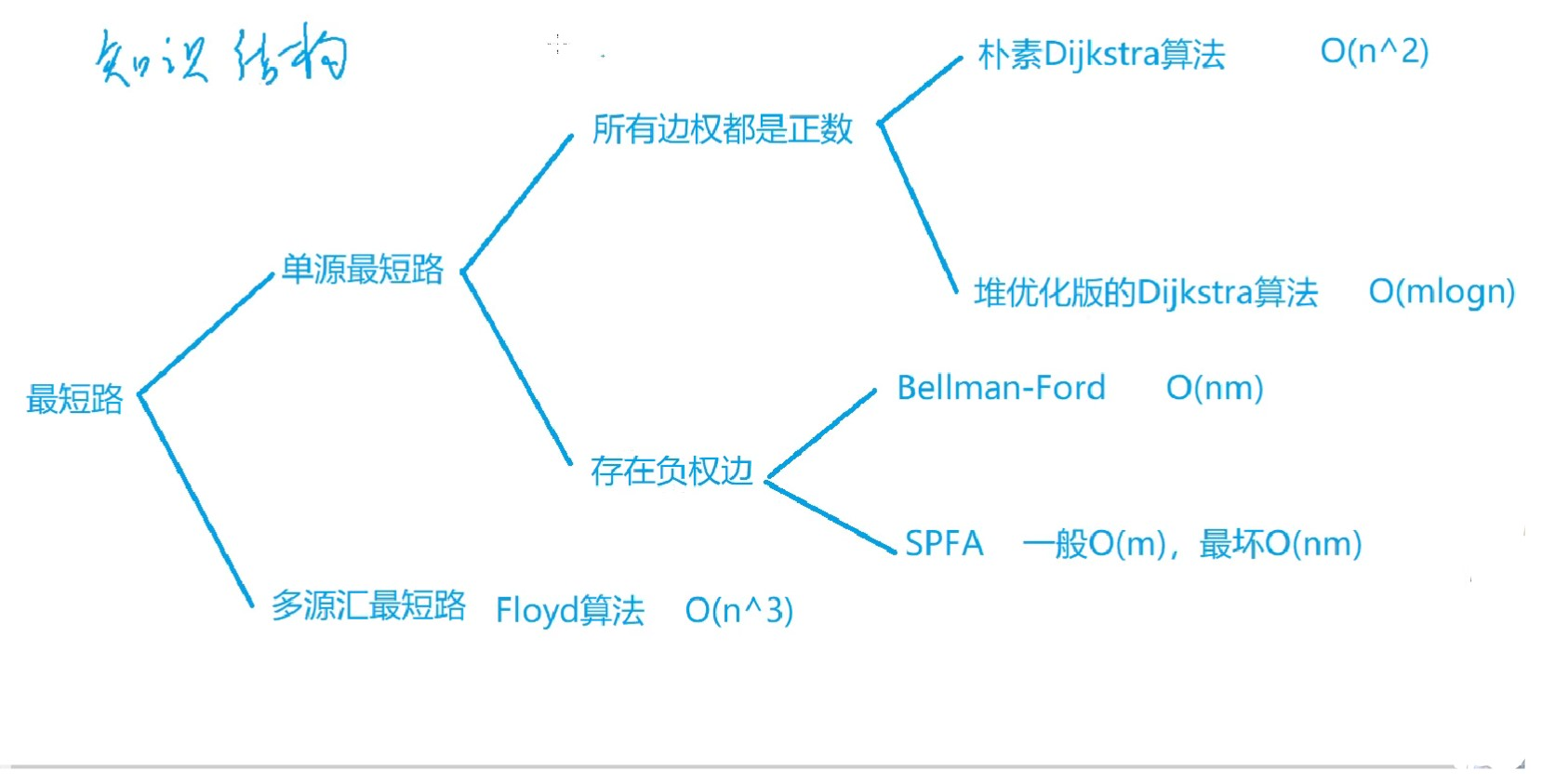
最短路问题总结见下图：(参考acwing视频)

image-20220616110720546

单源最短路

一个点到其他所有点的最短路

所有边权都是正数

n为点数，m为边数

  • 朴素dijkstra算法：O(n^2)

*如果是稠密图(m ~ n^2)*，尽量使用朴素dijkstra算法，其算法流程如下：

  1. 初始化：dist[1]=0, dist[i] = 正无穷，S=当前已确定最短路的点的集合{}
  2. n次迭代：
    • for i : 1~n 在不在S中的点中找到最小值
    • 将距离最短的点加入S（基于贪心的思想）
    • 使用t更新其他点的距离

因为是稠密图，所有推荐用邻接矩阵来存，存在重边的话，就只保留距离最短的那条边即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<cstring>
using namespace std;
const int N = 510;
int n,m;
int g[N][N];
int dist[N];
bool st[N];

int dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
                t= j;
        st[t] = true;
        for(int j=1;j<=n;j++)
            dist[j] = min(dist[j],dist[t]+g[t][j]);
    }
    
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}
int main(){
    scanf("%d%d", &n,&m);
    memset(g, 0x3f, sizeof g);
    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = min(g[a][b],c);
    }
    int t = dijkstra();
    printf("%d\n",t);
    return 0;
}
  • 堆优化版的dijkstra算法：O(mlogn)

如果是稀疏图(m ~ n)，用邻接表来存，那么应该用堆优化版dijkstra算法

image-20220914154000699

  • 堆

    • 手写堆

    • 优先队列（直接用STL即可，有可能有冗余）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int N = 150010;
int h[N],e[N],ne[N],w[N],idx;
typedef pair<int,int> PII;

int dijkstra(){
    memset(dist, 0x3f, sizeof dist);
    dist[1]=0;
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1});
    while(heap.size()){
        auto t = heap.top();
        heap.pop();
        int ver = t.second;
        int dis = t.first;
        if(st[ver]) continue;
        st[ver] = true;
        for(int i = h[ver];i!=-1;i=ne[i]){
            int j  = e[i];
            if(dist[j]>dis+w[i]){
                heap.push({dist[j],j});
            }                    
        }
    }
    
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

存在负权边

若能求出最短路，对应路径内中一定没有负权回路

  • Bellman-Fold ：O(nm)

外层循环n次，内层循环所有边，一个比较朴素的算法。

实际意义：迭代k次，dist[]存的是经过不超过k条边的从1到其他点的最短路距离，若第n次依然有更新，说明存在负权回路

应用场景：有边数限制的最短路（有负环也就无所谓了）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int bellman_ford(){
    memset(dist,0x3f,sizeof dist);
    for(int i=0;i<k;i++){
        memcpy(backup,dist,sizeof dist);
        for(int j=0;j<m;j++){
            int a = edges[j].a;
            int b = edges[j].b;
            int w = edges[j].w;
            dist[b] = min(dist[b],backup[a]+w);
        }
    }
    
    if(dist[n]>0x3f3f3f3f/2) return -1;
    return dist[n];
}
  • SPFA： 一般O(m) ，最坏O(nm)

没有负环就可以用SPFA，99%情况下都可以用。

在同一次迭代，dist[b]要想变小，只有可能是dist[a]变小了。因此用一个队列，队列存的是所有变小的结点。只要队列不空，我们就取出队头，再更新t的所有出边。主要思路就是，更新过谁再拿它来更新别人。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int spfa(){
    memset(dist,0x3f, sizeof dist);
    dist[1]=0;
    queue<int>q;
    q.push(1);
    //存的是当前的数是不是在队列当中，防止存重复
    st[1] = true;
    
    while(q.size()){
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i=h[t];i!=-1;i=ne[i]){
            int j = e[i];
            if(dist[j]>dist[t]+w[i]){
                dist[j] = dist[t] + w[i];
                if(!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

spfa求负环

若cnt[x]>=n，说明存在负环。

image-20220914173710231

至少有两个点是相同的，意味着路径上存在着一个负环。（一定会变小，不然不会存在这个环）

多源汇总最短路

不止一个起点，任选两个点，从其中一个点到另一个点的最短路问题

Floyd算法：O(n^3)

采用动态规划的思想：d[i,j]存储所有边，floyd算法包含三重循环：

  • 第一重：k从1到n
  • 第二重：i从1到n
  • 第三重：j从1到n:
    • d(i,j) = min(d(i,j), d(i,k) + d(k,j))

最小生成树

对应的图基本都是无向图

Prim算法

朴素版：稠密图。O(n^2)

算法流程和dijkstra算法流程非常类似 。首先把所有距离初始化为正无穷。接下来是n次迭代：

  1. 找到集合外距离最近的点。(集合S表示当前已经在连通块中的所有点。)
  2. 把t加入到集合中去。
  3. 用t更新其他点到集合的距离。（最短距离）
image-20220915153409498

选择的点所对应的边(最短的边)加入生成树中去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <cstring>
const int N = 510,INF = 0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];
bool st[N];

int prim(){
    memset(dist,0x3f,sizeof dist);
    int res = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        for(int j=1;j<=n;j++){
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
                t=j;
        }

        if(i && dist[t]==INF) return INF;
        if(i) res += dist[t];
        st[t] = true;
        for(int j=1;j<=n;j++){
            dist[j] = min(dist[j],g[t][j]);
        }
    }
    return res;
}

int main(){
    scanf("%d%d",&n,&m);
    memset(g,0x3f,sizeof g);
    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=g[b][a]=min(g[a][b],c);
    }
    
    int t = prim();
    if(t==INF) puts("impossible");
    else printf("%d\n",t);
}

堆优化版: 稀疏图。O(mlogn) 一般不会用到。

Kruskal算法

O(mlogm)

经验论：若是稀释图用kruskal算法，稠密图用Prim算法

  1. 将所有边按权重从小到大排序（快排，算法瓶颈O(mlogm)）
  2. 枚举每条边，若当前a,b不连通，将这条边加入集合中（并查集,O(m)）

简单而优美的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//只需要把每条边存下来就可以了，不需要用邻接表或邻接矩阵
const int N = 100010;
int n,m;
int p[N];
struct Edge{
    int a,b,w;
    bool operator<(const Edge &W) const{
        return w<W.w;
    }
}edges[N];

int find(x){
    if(x!=p[x]) p[x] = find(p[x]);
    return p[x];
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        int a,b,w;
        scanf("%d%d%d",&a,&b,&w);
        edges[i] = {a,b,w};
    }
    
    sort(edges,edges+m);
    
    for(int i=1;i<=n;i++) p[i]=i;
    int res = 0, cnt = 0;
    for(int i=0;i<m;i++){
        int a = edges[i].a,b = edges[i].b,w=edges[i].w;
        a = find(a),b = find(b);
        if(a!=b){
            res+=w;
            cnt++;
            p[a] =b;
        }
    }
    
    if(cnt<n-1) puts("impossible");
    else printf("%d\n",res);
    
    return 0;
}

二分图

概念：可以将所有点划分到两个集合，使得所有边都是在集合之间的，集合内部没有边。

染色法

给定一个图，判断它是不是二分图。

  • 时间复杂度：O(n+m)
  • 重要性质：一个图是二分图当且仅当图中不含奇数环。
  • 深度优先遍历：若在染色过程中出现了矛盾，就说明不是二分图

遍历每个点，如果该点未染色，那么深度遍历该点：dfs(i,1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
const int N = 100010, M = 200010;
int n,m;
int h[N],e[M],ne[M],idx;
int color[N];

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool dfs(int u, int c){
    color[u] = c;
    for(int i = h[u];i!=-1;i=ne[i]){
        int j = e[i];
        if(!color[j]) {
            if(!dfs(j,3-c)) return false;
        }
        else if(color[j]==c) return false;
    }
    return true;
}

int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    
    while(m--){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b),add(b,a);
    }
    bool flag;
    for(int i=1;i<=n;i++)
        if(!color[i]){
            if(!dfs(i,1)){
                flag = false;
                break;
            }
        }
    if(flag) puts("Yes");
    else puts("No");
}

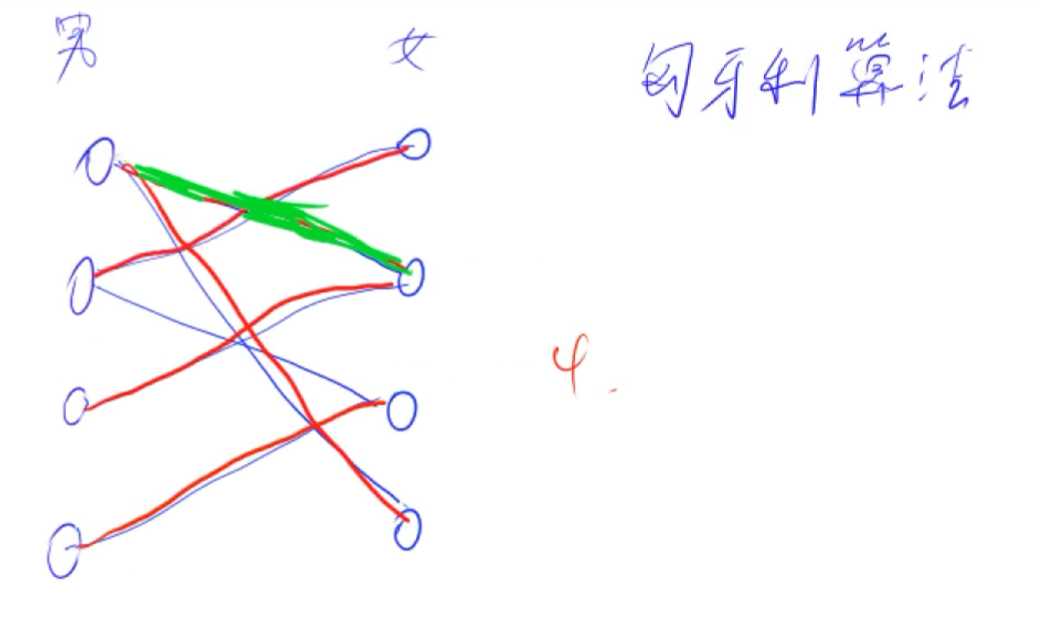
匈牙利算法

  • 时间复杂度：O(nm)

  • 给定一个二分图，求最大匹配的数量。匹配成功：没有两条边共用一个点

  • 存的时候，只需要存左边指向右边的边即可，match存的是右边点当前匹配的点，

image-20220915170431922 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int N = 510, M= 100010;
int n2,n2,m;
int h[N],e[M],ne[M],idx;
//match存的是右边的点对应的点
int match[N];
//判重，每次不要重复搜一个点
bool st[N];

bool find(int x){
    for(int i=h[x];i!=-1;i=ne[i]){
        int j = e[i];
        if(!st[j]){
            st[j] = true;
            if(!match[j]||find(match[j])){
                match[j] = x;
                return true;
            }
        }
    }    
    return false;       
}


int main(){
    scanf("%d%d%d",&n1,&n2,&m);
    memset(h,-1,sizeof h);
    
    while(m--){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
    }
    
    int res = 0;
    for(int i=1;i<=n1;i++){
        //表示这些右边的点还没有考虑过（保证每个右边的点只考虑一遍）
        memset(st,false,sizeof st);
        if(find(i)) res ++;
    }
    printf("%d\n",res);
}

第五讲 数论

质数

质数和和数是针对严格大于1的整数定义的，如果只包含1和本身两个约数，就被称为质数，否则为和数。

质数的判定

  • 试除法 O(n)
1
2
3
4
5
6
bool is_prime(int n){
    if(n<2) return false;
    for(int i=2;i<n;i++)
        if(n%i==0) return false;
    return true;
}

我们可以发现n的所有约数都是成对出现的，即若d为n的约束，那么n/d也为n的约数。所以我们不需要枚举所有数，只需要枚举的数即可，也就是说d只需枚举到即可

  • 优化 O()

不推荐使用sqrt(n)这个函数，也不推荐i*i<=n的写法，因为可能存在溢出风险，所以推荐写法为：i<=n/i

分解质因数

  • 试除法 O(n)

从小到大尝试n的所有因数，因为每次都会把因子除干净，所以不用担心满足n%i==0的数i会是和数。

1
2
3
4
5
6
7
8
9
10
11
12
void divide(int n){
    for(int i=2;i<n;i++){
        if(n%i==0){ // i 一定是质数
            int cnt = 0;
            while(n%i==0){
                n/=i;
                cnt++;
            }
            printf("%d %d",i,cnt);
        }
    }
}
  • 优化 最坏O()

hints: n中最多只包含一个大于sqrt(n)的质因子，所以可以枚举所有小于sqrt的质因子，如果最后剩下的因子n，若大于1直接输出即可。

  • 优化 O(logn)

求从1~n的所有质数

  • 筛法 O(nlogn)
1
2
3
4
5
6
7
8
9
10
11
bool st[N]; //为false代表没有被筛掉
int prime[N];
void get_prime(int n){
    int cnt = 0;
     for(int i=2;i<=n;i++){
         if(!st[i]){
             prime[cnt++]=i;
         }
         for(int j=i+i;j<=n;j+=i) st[j] = true;
     }
}
  • 优化：埃氏筛法 O(nloglogn)

根据基本分解定理，每个数只需要被素数筛掉就可以了，所有可以把第二个循环放到if里。

1
2
3
4
5
6
7
8
9
10
11
bool st[N]; //为false代表没有被筛掉
int prime[N];
void get_prime(int n){
    int cnt = 0;
     for(int i=2;i<=n;i++){
         if(!st[i]){
             prime[cnt++]=i;
             for(int j=i+i;j<=n;j+=i) st[j] = true;
         }      
     }
}
  • 线性筛法
1
2
3
4
5
6
7
8
9
void get_primes(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0;primes[j] <= n/i ; j++){
            st[primes[j]*i] = true; 
            if(i%primes[j] == 0) break;
        }
    }
}

正确性证明：

论断：如果是和数，只会被最小质因子筛掉，且一定能被筛掉

  1. 从小到大枚举所有质数，每一次把当前质数同i的乘积筛掉

  2. 第一次出现i%primes[j] == 0发生时意味着primes[j]一定是i的最小质因子，那么primes[j]也一定是primes[j]*i的最小质因子

  3. 若我们没有枚举到i的任何一个质因子，说明primes[j]一定小于i的所有质因子，所有primes[j]也一定是primes[j]*i的最小质因子

  4. 对于一个和数x，假设pj是x的最小质因子，当i（一定会）枚举到x/pj时，就会把x筛掉

线性筛法为什么是线性的？

每个数都只有一个最小质因子，每个数也只用最小质因子来筛，所以每个数只会被筛一次，所以是线性的。不加break就可能重复筛。

约数

求所有约数

  • 试除法+优化
1
2
3
4
5
6
7
8
9
10
11
vector<int> get_divisors(int n){
    vector<int> res;
    for(int i=1;i<=n/i;i++){
        if(n%i == 0){
            res.push_back(i);
            if(i!=n/i) res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

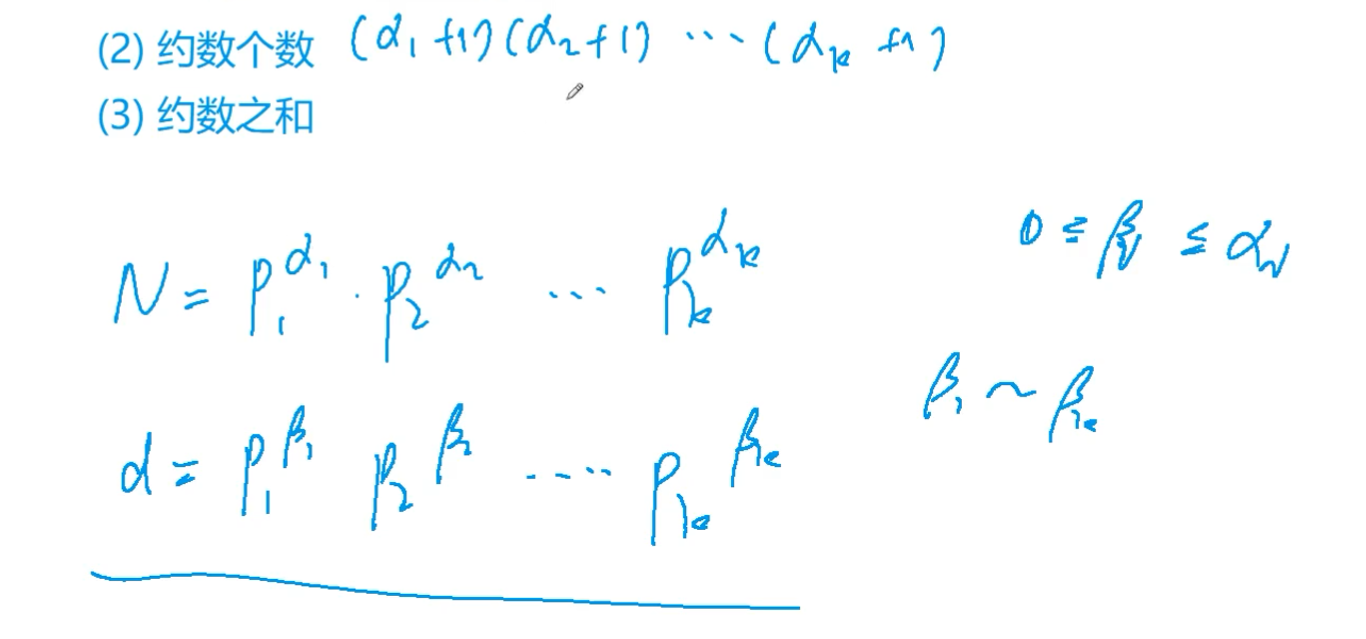
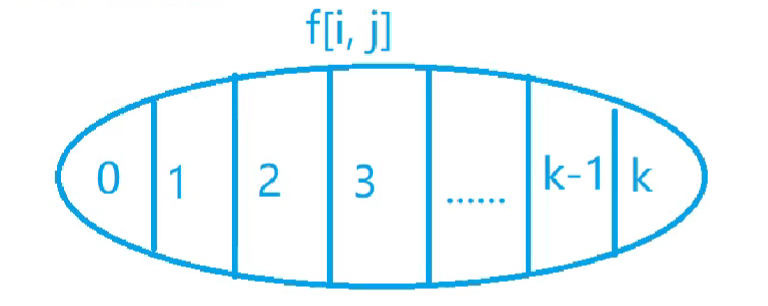
求一个数的约数个数

image-20220625171427739

n的每一个约数d就和我们从到的一种选法一一对应，所以约数个数为所有选法数量：$(\alpha_1+1)(\alpha_2+1)…(\alpha_{k-1}+1)(\alpha_k+1)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int main(){
    int n;
    cin>>n;
    unordered_map<int,int> map;
    
    while(n--){
        int x;
        cin>>x;
        for(int i=2; i<=x/i; i++){
            int cnt = 0;
            while(x%i==0){
                cnt++;
                x/=i;
            }
            map[i]+=cnt;
        }
        if(x>1) map[x]+=1;
    }
    LL res = 1;
    for(auto prime:map) res = res * (prime.second+1) % mod;
    cout<<res<<endl;
}

求一个数的约数之和

image-20220625172930529

每个约数均不相同，且是选法数量之一。

while(a--) t = t*p+1可以方便的求等比数列的和，其中a为指数，p为底数，也可以用公式做（尝试）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int main(){
    int n;
    cin>>n;
    unordered_map<int,int> map;
    
    while(n--){
        int x;
        cin>>x;
        for(int i=2; i<=x/i; i++){
            int cnt = 0;
            while(x%i==0){
                cnt++;
                x/=i;
            }
            map[i]+=cnt;
        }
        if(x>1) map[x]+=1;
    }
    LL res = 1;
    for(auto prime:map) {
        LL temp = 0;
        prime.second+=1;
        while (prime.second--) {
            temp = (temp * prime.first + 1) % mod;
        }
        res = res * temp % mod;
    }
    cout<<res<<endl;
}

求最大公约数

辗转相除法

核心：（a，b）= （b，a mod b)

1
2
3
int gcd(int a,b){
    return b ? gcd(b,a mod b) : a;
}

欧拉函数

概念：

记号为，表示为1~n中与n互质的数的个数

例如。

欧拉公式：

首先对n分解质因数 $p_1^{\alpha_1}p_2^{\alpha_2}…p_k^{\alpha_k}，根据公式即可计算出结果\phi(n) = n(1-1/p_1)(1-1/p_2)…*(1-1/p_k) $

证明：

使用容斥原理可以证明

  1. 从1~n中去掉的所有倍数
  2. 加上所有的倍数（加回多减的）
  3. 减去所有$pipjpk$的倍数
  4. 以此类推

把欧拉公式展开和容斥原理的式子是等价的：

image-20220920163736057

可画图理解：

image-20220920163535256

筛法求欧拉函数 O(n)

某些情况下，需要求出1~n中每一个数的欧拉函数。若用公式法需要O(N*sqrt(N))的复杂度

若用线性筛法，可以用O(n)的复杂度计算出每一个数的欧拉函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void get_eulers(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]) {
            // 如果一个数i是质数，那么欧拉函数就是i-1
            primes[cnt++] = i;
            phi[i] = i-1;
        }
        for(int j = 0;primes[j] <= n/i ; j++){
            st[primes[j]*i] = true;
            if(i%primes[j] == 0) {
                phi[primes[j]*i] = primes[j]*phi[i];
                break;
            }
            phi[primes[j]*i] = (primes[j]-1)*phi[i];
        }
    }
}

应用场景：欧拉定理

若a与n互质，

注：等于号代表同余

欧拉定理的特例：费马小定理

若n为质数，假设a与n互质，那么有

快速幂

  • 在**O(log k)**的情况下快速地求出的结果。

  • 核心思路：反复平方法

我们先要预处理出来这些值：

image-20220920171218205

如何组合成ak?

把拆成若干个上面的预处理出来的数的乘积的形式（用2进制表示即可），即把k换成2进制即可。

image-20220920171538284 image-20220920171725759

所有问题等价于：底数相同，将k表示成以2为底的指数的和

1
2
3
4
5
6
7
8
9
10
typedef Long Long LL;
int qmi(int a , int k, int p){
    int res = 1;
    while(k){
        if(k&1) res = (LL)res*a%p;
        k>>=1;
        //每个数都是前面的数的平方模p
        a=(LL)a*a%p;
    }
}

快速幂求乘法逆元

其实本质上就是一个快速幂

证明：

希望把除法变乘法：

左右两边同乘以b：

因而

之后可以用费马定理来解决，但注意m要为质数，且b与m互质

因而

所以b的模m的逆元为

扩展欧几里得算法

裴蜀定理

有任意一对正整数a、b，那么一定存在整数x、y，使得ax+by = gcd(a,b)。a,b所能凑出来的所有数都是最大公约数的倍数，所以能凑出来的最小的数就是最大公约数。

注：x，y可取负整数

解决什么问题

为裴蜀定理构造解

1
2
3
4
5
6
7
8
9
int ext_gcd(int a, int b, int &x, int &y){
     if(!b){
         x = 1,y=0;
         return a;
     }
     int ans = ext_gcd(b,a%b,y,x);
     y -= a/b *x;
     return ans;
}

简单应用：求解线性同余方程

等价于，所以若(a,-m)|b成立则有解，可以用扩展欧几里得算法算出x；否则无解

中国剩余定理

求解一元线性同余方程组，m1-k两两互质

image-20220629151521256

通解的构造方法：

image-20220629151745571

求逆元ti可以用扩展欧几里得算法解出：

image-20220629153424432

通解构造的正确性可通过带入法进行验证。

高斯消元

线性代数相关知识

一般可以再O(n^3)的时间复杂度内，求解n个方程n个未知数的多元线性方程组。

解的情况

  • 无解：通过行变换推出0=非0，矛盾
  • 无穷多组解：0=0，n个未知数，n-1个方程
  • 唯一解：完美阶梯形

注：初等行变换不改变方程组的解，而且可以将方程组变为上三角的形式：

image-20220704103319314

算法流程

  • 从不固定的方程里，枚举每一列，找出绝对值最大的这一行（处理精度问题）
  • 将这行换到上面去
  • 将该行第一个数变为1
  • 将下面所有行的当前列消成0
  • 若有唯一解，那么用消元法即可得到解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//因为c++浮点数存的时候是有误差的，所以不能直接判断0，而是应该判断是不是小于一个很小的数
const double eps = 1e-6;

double a[N][N] ;
int gauss(){
    int c,r;
    // 从第0行，第0列开始枚举
    for(c=0,r=0;c<n;c++){
        int t = r;
        for(int i = t; i<n;i++)
            if(fabs(a[i][c])>fabs(a[t][c]))
                t = i;
        if(fabs(a[t][c])<eps) continue;
    	for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);
    	for(int i=n;i>=c;i--) a[r][i] /= a[r][c];
        for(int i=r+1;i<n;i++)
            if(a[i][c] > eps)
                for(int j=n;j>=c;j--)
                    a[i][j] -= a[r][j] * a[i][c];
        r++;               
    } 
    
    if(r<n){
        for(int i=r;i<n;i++)
            if(fabs(a[i][n])>eps)
                return 2; //无解
        return 1; //有无穷多组解
    }
    return 0;//有唯一解
}

组合数

公式法

由公式，可以计算出组合数：

1
2
3
4
5
6
7
8
9
int p;
int C(int a, int b){
    int res = 1;
    for(int i=1,j=a;i<=b;i++,j--){
        res = (LL)res*j % p;
        res = (LL)res *qmi(i,p-2) % p;
    }
    return res;
}

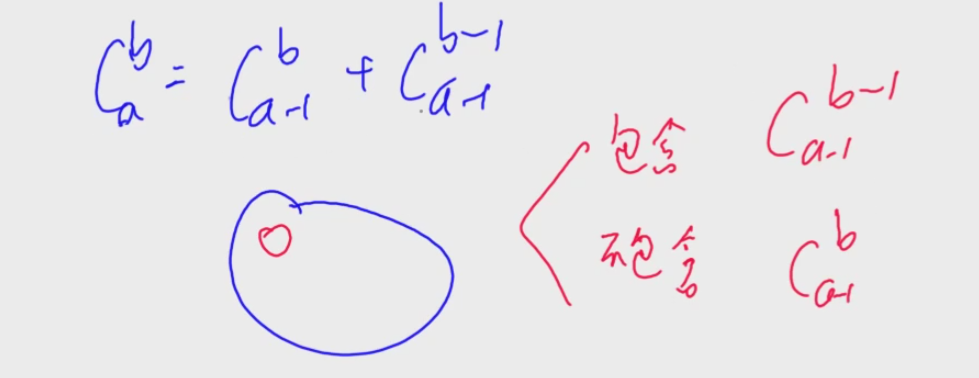
递推式法

10万组询问，a,b范围较小：1<= a,b<=2000

根据递推式，先预处理出所有的 组合数（两重循环即可），到时候查表即可在O(ab)的时间复杂度下完成计算。

image-20220704113215891 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
using namespace std;
const int K = 2010;
const int mod = 1e9+7;
typedef long long LL;

int com[K][K];

int main(){
    int n;
    cin>>n;
    for(int i=1;i<K;i++){
        com[i][0]=1;
        com[i][i]=1;
        for(int j=1;j<i;j++){
            com[i][j] = (com[i-1][j]+com[i-1][j-1])%mod;
        }
    }
    while(n--){
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n",com[a][b]);
    }
    return 0;
}

预处理公式法

1万组询问，a,b范围适中：1<=a,b<=1e5

根据公式，预处理出中间的一步:阶乘。用fact[i]表示i! mod 10^9+7，infact[i]表示 mod 10^9+7

也可以用查表的方式O(NlogN)来求 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
using namespace std;
typedef long long LL;
const int mod = 1e9+7;
const int N = 100010;
int fact[N];

int qmi(int a , int k, int p){
    int res = 1;
    while(k){
        if(k&1) res = (LL)res * a % p;
        k>>=1;
        a = (LL)a * a % p;
    }
    return res;
}
int main(){
    fact[0]=1;
    for(int i=1;i<=N;i++)
        fact[i] = (LL)i*fact[i-1] % mod;
    int n;
    scanf("%d",&n);
    while(n--){
        int a,b;
        scanf("%d%d",&a,&b);
        int infact1 = qmi(fact[a-b],mod-2,mod);
        int infact2 = qmi(fact[b],mod-2,mod);
        int com = (LL)fact[a] * infact1 % mod * infact2 % mod;
        printf("%d\n",com);
        // printf("%d %d %d\n",fact[a],infact[a-b],infact[b]);
    }
    
    
    return 0;
}

卢卡斯定理

20组询问，a,b范围巨大：1<=a,b<=10^18，1<=p<=10^5

$C^b_a = C^{b%p}{a%p}*C^{b/p}{a/p} (%p)$

算法复杂度为O()，前半部分为递归层数，后半部分为每层递归里求组合数的复杂度；

证明可参考该博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
using namespace std;
typedef long long LL;

int qmi(int a, int k, int p){
    int res = 1;
    while(k){
        if(k&1) res = (LL)res * a %p;
        k>>=1;
        a =(LL)a * a % p;
    }
    return res;
}



int C(int a, int b,int p){
    if(b>a) return 0;
    int res = 1;
    for(int j=1,i=a;j<=b;j++,i--){
        res =  (LL)res * i % p;
        res = (LL)res * qmi(j,p-2,p) % p;
    }
    return res;
}

int lukas(LL a, LL b, int p){
    if(a<p && b<p) return C(a,b,p);
    return (LL)C(a%p,b%p,p) * lukas(a/p,b/p,p) % p;
}

int main(){
    int n;
    cin>>n;
    while(n--){
        LL a,b;
        int p;
        scanf("%ld%ld%d",&a,&b,&p);
        printf("%d\n",lukas(a,b,p));
    }
    return 0;
}

分解质因数+高精度

先把分解质因数 ，即$p_1^{\alpha_1}p_2^{\alpha_2}…*p_k^{\alpha_k}$，之后只需要实现一个高精度乘法即可。

  • 对每一个数分解质因数，效率较低O(NlogN)
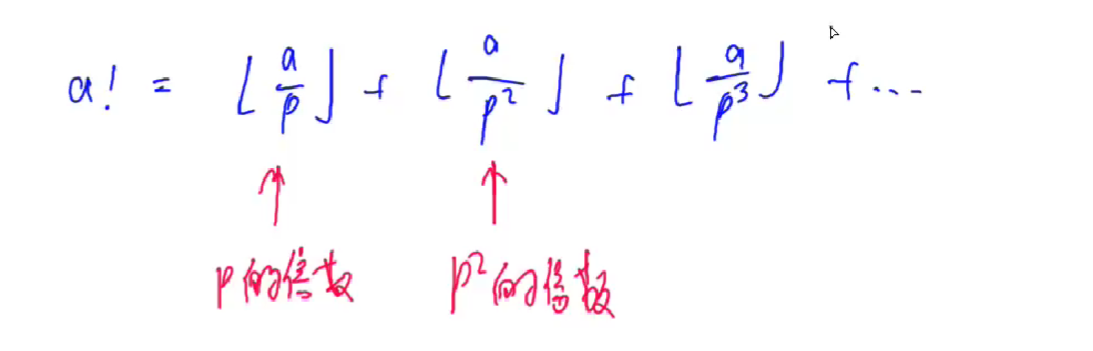
  • 改进：先处理出所有的质因子（筛素数），再求出这个质因子的次数是多少。由公式，求p次数的方法为，先看分子里p的个数，再看分母里p的个数，差值即为真正的p的个数。那么如何得到阶乘里p的个数呢？通过下面的算法可以巧妙地计算出阶乘里p的个数：
image-20220926164810125 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<vector>
#include<iostream>
using namespace std;
const int N  = 5010;
int prime[N];
bool st[N];
int cnt=0;
// 暴力解法
// 分别求出1~n的质因子p的数量再相加：O(NlogN)
int get(int n, int p){
    for(int i=1;i<=n;i++){
        int t = i;
        while(t%p==0){
           t/=p;
           cnt[i]++;
        }
    }
    int res = 0;
    for(int i=1;i<=n;i++){
        res += cnt[i];
    }
}

// 优化
// 计算出阶乘里p的个数O(logN)
int get(int n, int p){
    int res = 0;
    while(n){
        res += n/p;
        n/=p;
    }
    return res;
}
// 筛素数
void get_prime(int n){
     st[1] = true;
     for(int i=2;i<=n;i++){
         if(!st[i]){
             prime[cnt++]=i;
         }
         for(int j=0;prime[j]<=n/i;j++){
             st[prime[j]*i] = true;
             if(i%prime[j]==0) break;
         }
         
     }
}

vector<int> multiply(vector<int>  a, int b){
    int c = 0;
    vector<int> C;
    for(int i=0; i<a.size()||c;i++){
        if(i<a.size()) c+=a[i]*b;
        C.push_back(c%10);
        c/=10;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}
int main(){
    vector<int> base;
    base.push_back(1);
    get_prime(N);
    int a,b;
    cin>>a>>b;
    for(int i=0;i<cnt;i++){
        int p = prime[i];
        int k = get(a,p)-get(b,p)-get(a-b,p);
        while(k--) base = multiply(base,p);
    }
    
    for(int i=base.size()-1;i>=0;i--) printf("%d",base[i]);
    return 0;
}

卡特兰数

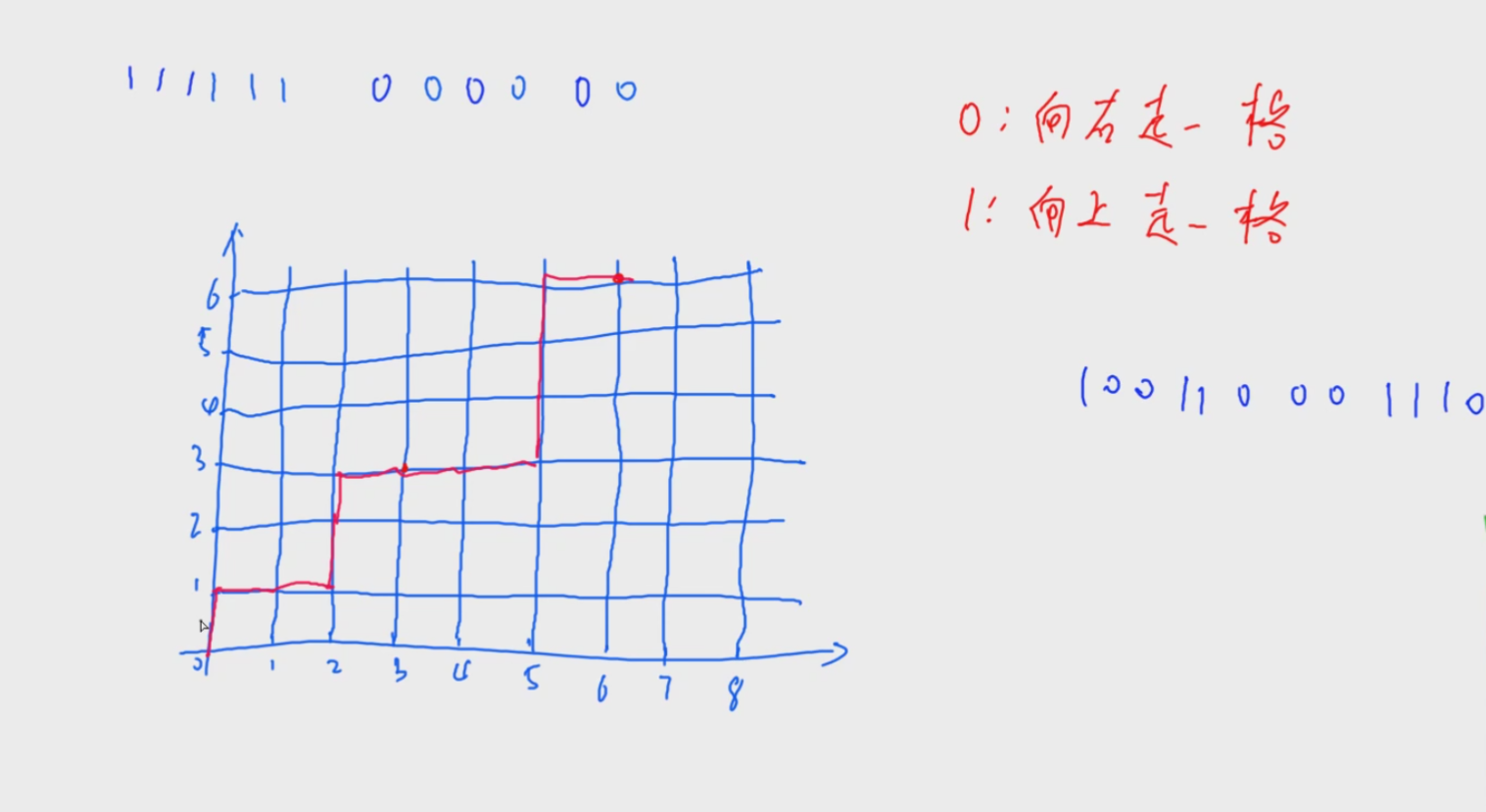
  1. 满足条件的01序列

给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

image-20220927151801338

每一个数列都对应一个从（0，0）到（6，6）的路径，反过来也成立。

$C_{2n}^{n}-C^{n-1}{2n}=1/(n+1)*C^n{2n}$

应用

火车进站问题

合法括号序列问题

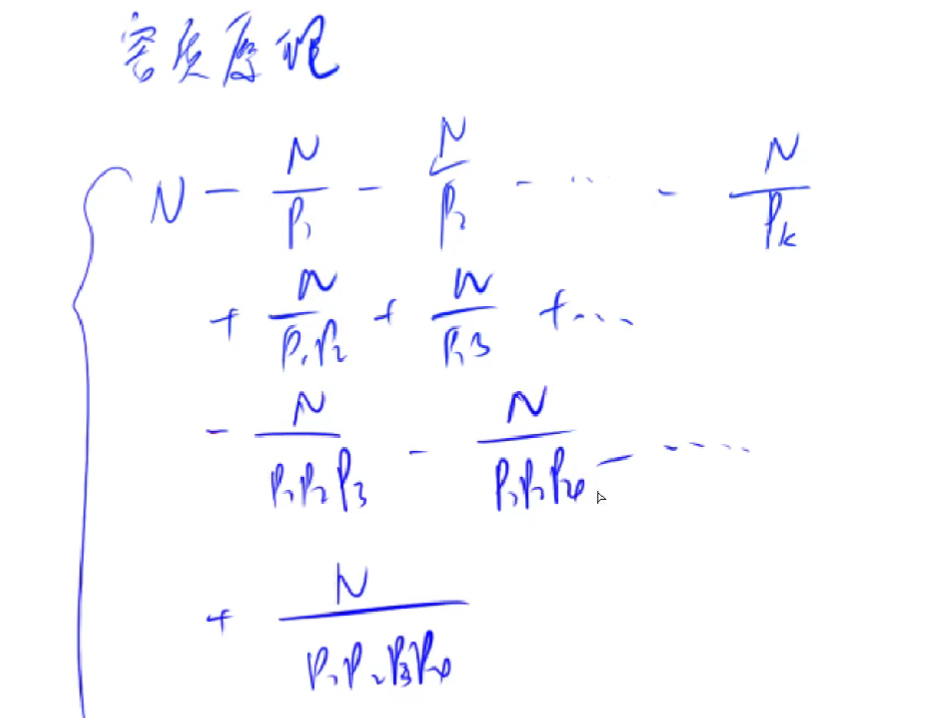
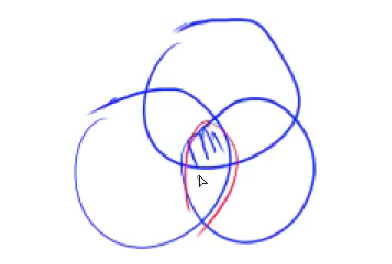
容斥原理

对于n个圆，计算其所占的面积 ，数字代表i个圆的交集的组合。

对于集合来讲，集合的个数也满足上式。

上式一共有多少项？

从n个数里挑任意多个数的方案数

所以一共有项，所以时间复杂度为

为什么是+、-、+、-？

image-20220711151708971

根据组合恒等式，对于集合中的某个数x，它在k个集合中出现过，它只会在右边的等式里计算一次。

实际应用

给定一个整数 n 和 m个不同的质数，请你求出 1∼n中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。

时间复杂度O(2^m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
using namespace std;
const int N = 20;
int p[N];

int main(){
    int n,m;
    cin>>n>>m;
    int res =0;
    for(int i=0;i<m;i++) scanf("%d",&p[i]);
    for(int i=1;i<1<<m;i++){
        int t = 1;
        int cnt = 0;
        for(int j=0;j<m;j++){
            if(i>>j&1) {
                cnt++;
                t*=p[j];
                if ((LL)t*p[j]>n) {
                    t=-1;
                    break;
                }
            }
        }
        if(t!=-1){
            if(cnt % 2) res += n/t;
            else res -= n/t;
    	}
    }
    cout<<res<<endl;
    return 0;
}

博弈论

公平组合游戏ICG

若一个游戏满足：

  1. 由两名玩家交替行动；
  2. 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关;
  3. 不能行动的玩家判负；
    则称该游戏为一个公平组合游戏。下面介绍的Nim游戏即为公平组合游戏。但围棋等游戏不满足2，3，判胜条件比较复杂。

有向图游戏

给定一个有向无环图，图中由唯一的一个起点，在起点上有一枚棋。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。任何一个公平组合游戏都可以转化为有向图游戏。具体方法：

  • 把每个局面看成图中的一个节点，并且从每一个局面沿着（有向边）合法行动能够到达下一个局面。

Nim游戏

给定n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子，最后无法进行操作的人视为失败。

  • 先手必胜状态：可以走到某一个必败状态

  • 先手必败状态：every state you go is a win state, i.e. 走不到任何一个必败状态

  • so how to judge the win or lose state ?

定理：对于n堆石子(a1,a2,a3,…,an)，如果a1^a2^…^an=0，先手必败，否则先手必胜
provement:

  1. 0^0^0^…^0=0
  2. a1^a2^…^an = x != 0, can go to all 0 state: retrieve ai-ai^x
  3. a1^a2^…^an=0, can go to none 0 state

思考题：台阶Nim游戏
hint: xor what numbers

集合-Nim游戏

  • Mex 运算：
    设S为一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：mex(S)=min{x}，x属于自然数且x不属于S

  • SG函数：

局面（状态）

SG（终点）=0；

每个状态的 SG（x）=mex{SG(y1),SG(y2),…,SG(yk)}; 其中y1-k为从x经过某些操作能到的局面（状态）

若SG(x)!=0，必胜，否则必败。
因为任何一种非0状态一定可以走到0状态，而从0状态只能走到非0状态。出生决定了最终的结果，即如果我一开始不是0，那么我未来永远都不是0；

extentison: if there is more than one graph. if one can operate on any graph, he will lose. Suppose we have n graphs to use, we xor all the SG values of the beginning nodes.
if SG(x1)^SG(x2)^…^SG(xn) ==0 lose, otherwise will win.

The provement is the same as the nim games;

  • Set Nim Game
    Given n piles of stones and a digit set of K different positive numbers. There are two players who can alternatively pick stones from any piles of stones. But the number of stones taken each time must belong to the digit set. The one who can’t make any actions will lose.(restrict the numbers of stones taken)
image-20220929123941913 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<cstring>
using namespace std;

const int N = 10010;
int sg(int x){
    if(f[x]!=-1) return f[x];
    unordered_set<int> S;
    for(int i=0;i<m;i++){
        int sum = s[i];
        if(x>=sum) S.insert(sg(x-sum));
    }

    for(int i=0;;i++)
        if(!S.count(i))
            return f[x] = i;

}

第六讲 动态规划基础

理解动态规划的思考方式

从集合的角度理解DP问题

  • 状态表示 f(i,j)（存的是所有选法的集合的最值），考虑清楚需要几维来表示我们的问题

    • 集合：每一个状态都是表明一个集合，在背包问题里表示所有选法的集合

      条件：

      • 只考虑前i个物品
      • 总体积不超过 j

    • 属性：集合的最大值，最小值，元素数量

  • 状态计算 ，如何将每个状态计算出来

    • 目标：求f(N,V)

    • 状态计算一般表示集合的划分：把当前集合划分为若干个更小的子集，使得每一个子集我们都可以由前面更小的状态计算得到

      例如f(i,j)可以包含两类：

      • 左边类是不包含第i个物品的选法
      • 右边类是包含第i个物品的选法

      实际的最大值是两类取一个max

DP问题的优化一般只是等价变形，所以写出朴素解法十分重要

DP问题一定要结合题目来理解，上面的思考方式就像是骨架，根据具体问题填补具体的血肉

背包模型

01背包问题

什么是01背包？

每件物品最多只能用一次

在背包容量的范围内如何挑选物品，让总价值最大

朴素做法

1
2
3
4
5
6
7
8
//枚举所有状态f[0,0]~f[n,m]
//其中f[0,0-m]表示考虑0件物品，总体积不超过0~m的最大价值是多少
//因此只需从1开始遍历即可
for(int i=1;i<=n;i++)
    for(int j=0;j<=m;j++){
        f[i][j] = f[i-1][j];
        if(j>=v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]] + w[i]);
    }

一维做法

第i层的状态只依赖于第i-1层；不超过的总体积j只依赖于<=j的状态，因此可以优化到一维来做

1
2
3
4
5
int f[N];//直接去掉一维
for(int i=1;i<=n;i++)
    for(int j=m;j>=v[i];j--){
        f[j] = max(f[j],f[j-v[i]]+w[i]);
    }

完全背包问题

每件物品可以用无限次

解题思路

分成若干组，分成k类：

image-20220714135234544

不妨设第i个物品选了k个

曲线救国：

  1. 去掉k个物品i
  2. 求Max，f[i-1,j-k*v[i]]
  3. 再加回来k个物品i

综上，f[i,j] = f[i-1,j-k*v[i]] + k * w[i]

朴素做法

1
2
3
4
5
//最坏情况下：O(n*m^2))
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++)
        for(int k=0;k*v[i]<=j;k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

二维做法

1
2
3
4
5
6
7
8
9
//f[i,j] = Max(f[i-1][j],f[i-1,j-v]+w,f[i-1,j-2v]+2w,f[i-1,j-3v]+3w,...)
//f[i,j-v] = Max(f[i-1][j-v],f[i-1,j-2v]+w,f[i-1,j-3v]+2w,...)
//f[i,j] = Max(f[i-1][j],f[i,j-v]+w);
//优化为二维
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++){
        f[i][j] = f[i-1][j];
        if(j>=v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
    }

一维做法

完全背包问题的终极解法

1
2
3
4
int f[N];
for(int i=1;i<=n;i++)
    for(int j=v[i];j<=m;j++)
        f[j] = max(f[j],f[j-v[i]]+w[i]);

多重背包问题

每件物品最多有Si个

解题思路

枚举第i个物品选多少个，根据第i个物品选多少个来将我们所有的选法分成若干种类别：

image-20220714145946121

其实就是朴素版本的完全背包问题：f[i,j] = f[i-1,j-k*v[i]] + k * w[i]

朴素版本

1
2
3
4
5
//最坏情况下：O(n*m^2))
for(int i=1;i<=n;i++)
    for(int j=0;j<=m,j++)
        for(int k=0;k<=s[i] && k*v[i]<=j ;k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

优化版本：二进制优化

c++1s最多算1亿次，超过一亿次会超时

从0~s中的任何一个数都可以被拼凑出来（由1，2，4，2^k, … , c）。

将s个物品i拆分程log(s)个新的物品，新的物品只能用一次

对所有这些新出来的物品做一遍01背包即可，时间复杂度为O(N*v*log(s))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>

using namespace std;

const int N = 11100,M=2010;
int v[N];
int w[N];
int f[N];

void backpack_multi_bin_Test() {
    int n, m;
    cin >> n >> m;
    //如果用三重循环，4亿的计算量很可能会爆掉
    //思路：将s[i]个相同的物品分解为多个不同的物品且每个物品只能取一次
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int a,b,s;
        cin >> a >> b >> s;
        int j;
        for (j = 1; j <= s; j *= 2) {
            cnt++;
            s-=j;
            v[cnt] = j * a;
            w[cnt] = j * b;
        }
        if(s){
            cnt++;
            v[cnt] = s*a;
            w[cnt] = s*b;
        }
    }

    for(int i=1;i<=cnt;i++)
        for(int j=m;j>=v[i];j--){
            f[j] = max(f[j], f[j-v[i]]+w[i]);
        }
    cout<<f[m]<<endl;
}

分组背包问题

有n组物品，同一组内的物品最多只能选一个

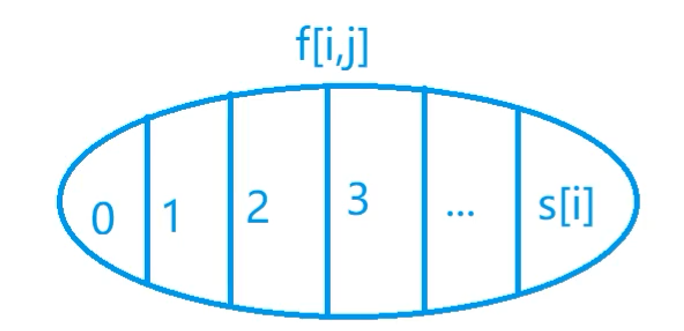
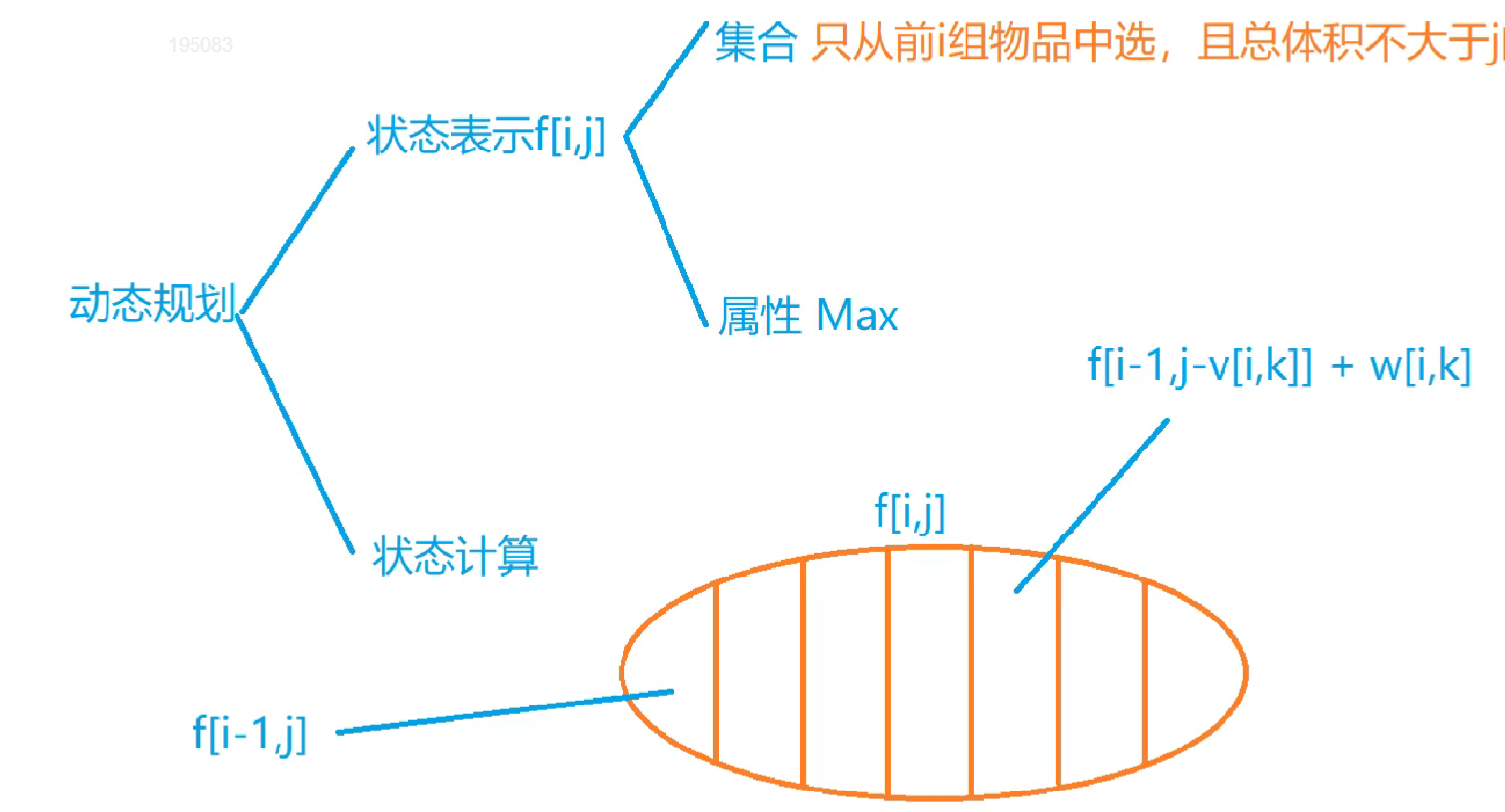
状态表示的集合：只能从前i组物品中选，且总体积不大于j的所有选法

枚举第i组物品选不选，选哪个

image-20220714155045511

朴素解法

1
2
3
4
5
6
7
for(int i=1;i<=n;i++)
    for(int j=0;j<=m;j++){
        f[i][j] = f[i-1][j];
        for(int k=0;k<s[i];k++){
            if(j>=v[i][k]) f[i][j] = max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
        }
    }

优化解法

1
2
3
4
5
6
int f[N];//直接去掉一维
for(int i=1;i<=n;i++)
    for(int j=m;j>=0;j--)
    	for(int k=0;k<s[i];k++){
            if(j>=v[i,k]) f[j] = max(f[j],f[j-v[i,k]]+w[i,k]);
        }

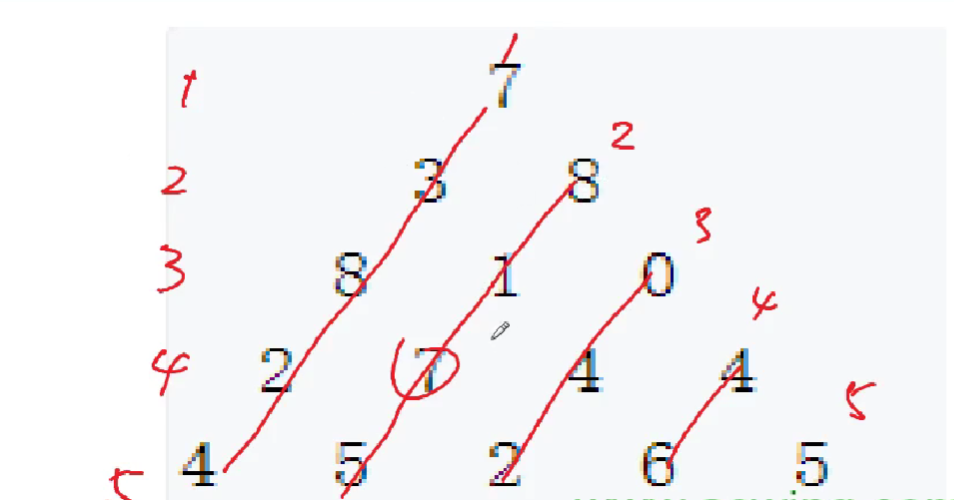
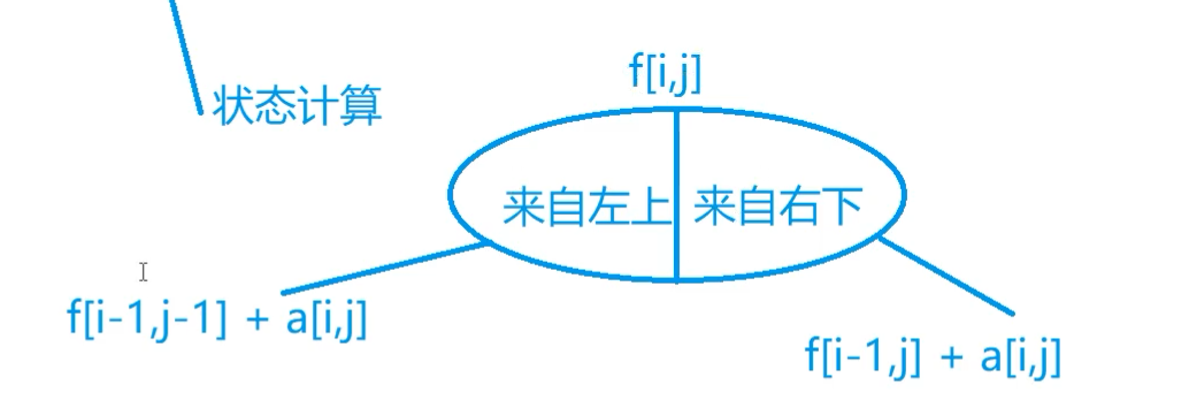
线性DP

数字三角形

从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至右下方的结点，一直走到底层。要求找到一条路径上的数字的和最大。

状态表示

image-20220718102743701
  • 集合：从顶点到(i,j)的所有路径
  • 属性：MAX

状态计算

image-20220718103338018

复杂度：状态数量*转移数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const int  N = 510,inf = -1e9;
int f[N][N];
int d[N][N];
void digi_Tran_Test(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            scanf("%d",&d[i][j]);
    for(int i=0;i<=n;i++)
        for(int j=0;j<=i+1;j++)
            f[i][j]= inf;
    f[1][1] = d[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++){
            f[i][j] = max(f[i-1][j-1],f[i-1][j])+d[i][j];
        }

    int res = inf;
    for(int i=1;i<=n;i++)
        res = max(res,f[n][i]);
    cout<<res<<endl;

}

最长上升子序列

给定一个数列，求数值严格单调递增的子序列的长度最长是多少

可以按照顺序跳着选择

状态表示

  • 集合：所有以第i个数为结尾的数值上升的子序列
  • 属性：子序列的最大长度

状态计算

image-20220718105358393

以倒数第二个数在哪个位置来进行划分，需满足数值严格单调上升（即第i个数大于倒数第二个数）

朴素版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int M = 1010;
int sta[M];
int sq[M];
void maxLenIncSubTest() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&sq[i]);
    for(int i=1;i<=n;i++) {
        sta[i] = 1;
        for (int j = 1; j < i; j++) {
            if(sq[j]<sq[i])
                sta[i] = max(sta[i],sta[j]+1);
        }
    }
    int res = 0;
    for(int i=1;i<=n;i++)
        if(res < sta[i]) res = sta[i];
    cout<<res<<endl;
}

优化版

如果数列过长，会爆掉，因此需要找到一个优化的算法。存所有不同长度的所有严格上升子序列的结尾的最小值。

image-20221008163234567

我们可以证明，随着长度的增加，结尾的最小值必然严格上升。假设长度为6的最小值等于长度为5的最小值，又严格上升子序列，因此第5个数比之前的长度为5的最小值还要小，产生了矛盾。因此长度为6的最小值一定大于长度为5的最小值。

对于当前的数ai，找到序列中最大的小于ai的数，假设是q[4]，则q[5]>=ai，也就是说ai不能接到长度>=5的子序列后边。也就是说以ai为结尾的子序列长度最大即为5。找出小于ai的最大的一个数可以用二分来做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int find_pos(int le, int ri, int tar){
    while(le<ri){
        int mid = le + ri + 1 >> 1;
        if (q[mid] < tar)
            le = mid;
        else ri = mid -1;
    }
    return le;
}

void maxlenII(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&nums[i]);
    q[0] = -pintf;
    int qLen = 0;
    for(int i=1;i<=n;i++){
        int pos = find_pos(0,qLen,nums[i]);
        q[pos+1] = nums[i];
        if(pos+1>qLen)  qLen = pos + 1;
    }
    cout<<qLen<<endl;
}

最长公共子序列

既是a的子序列，又是b的子序列的字符串长度的最大值。

状态表示

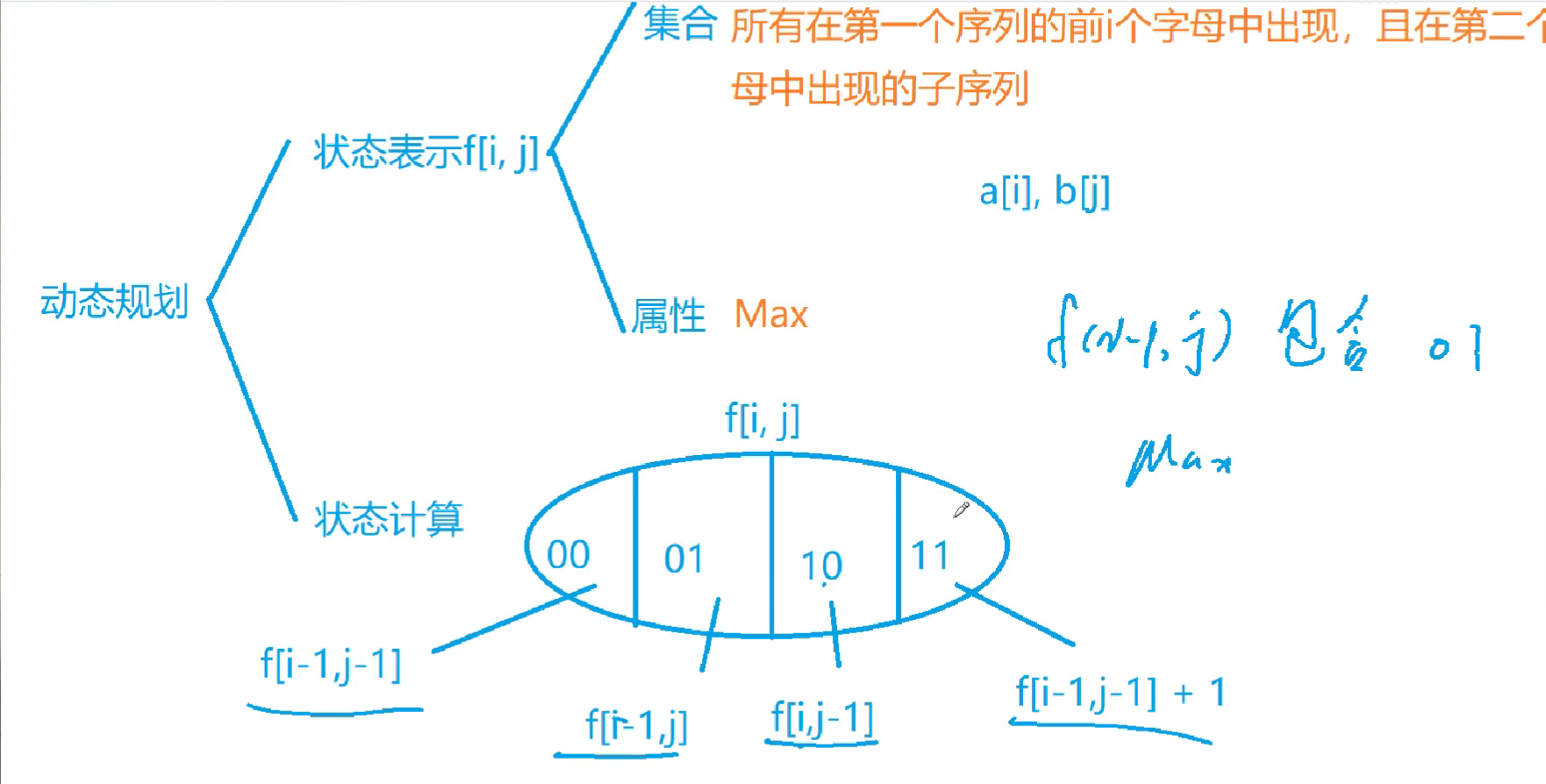
  • 集合：所有由第一个序列的前i个字母，和第二个序列的前j个字母的构成的公共子序列
  • 属性：公共序列的最大值

状态计算

求max是可以重复的，只要不漏掉某一元素即可

image-20220718143637328 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int M = 1010;
char a[M];
char b[M];
int st[M][M];
void maxCommenSubTest(){
    int n,m;
    cin>>n>>m;
    scanf("%s",a+1);
    scanf("%s",b+1);
    // A中前i个字符和B中前j个字符所构成的公共子序列的集合
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            st[i][j] = max(st[i][j-1],st[i-1][j]);
            if(a[i]==b[j]) st[i][j] = max(st[i][j],st[i-1][j-1]+1);
        }
    cout<<st[n][m]<<endl;
}

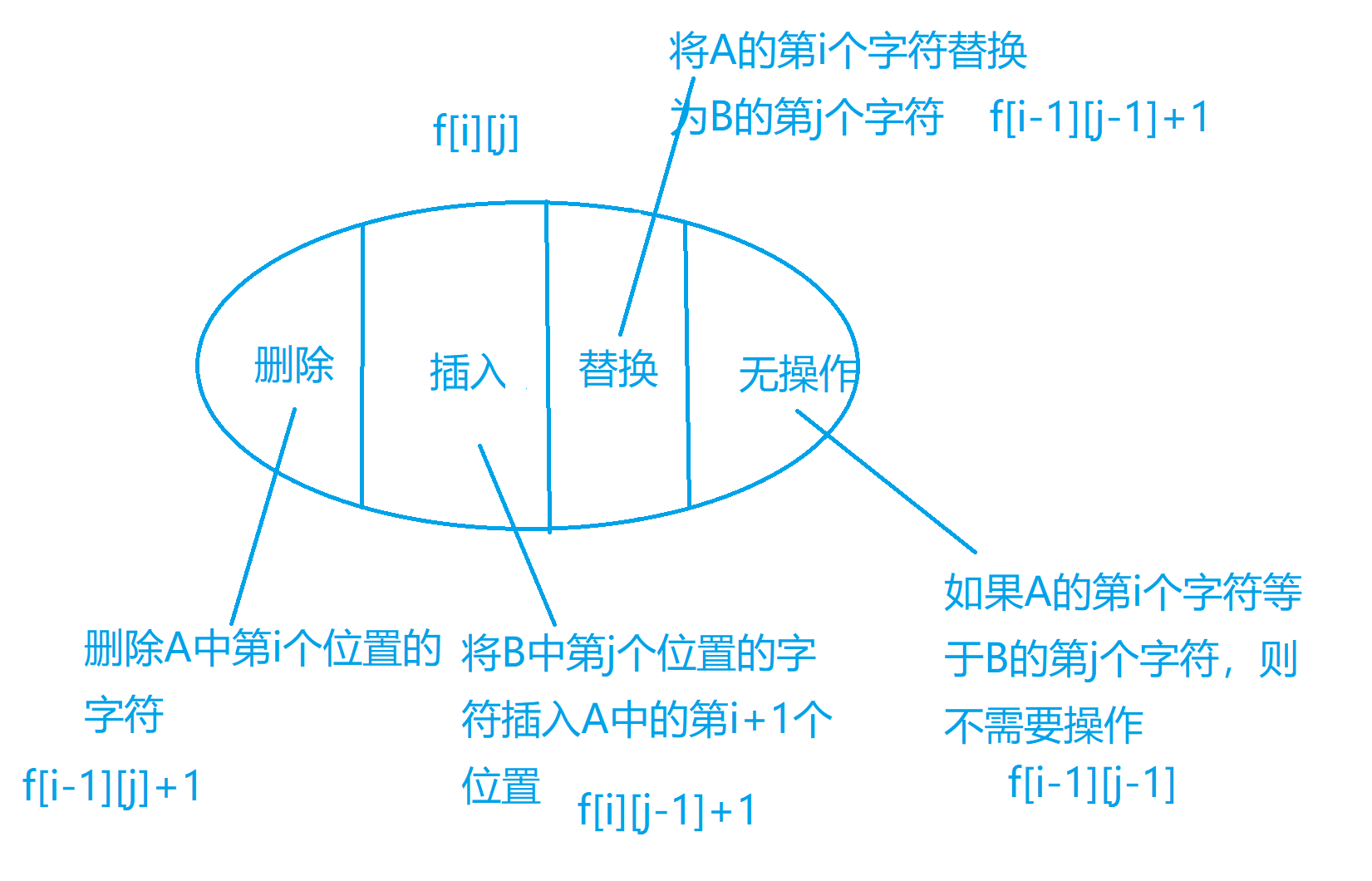
最短编辑距离

给定两个字符串A和B，现在要将A经过若干操作变为B，可进行的操作：

  1. 删除
  2. 插入
  3. 替换

求变换所需的最小操作次数。

状态表示

  • 集合：将A的前i个字符变为B的前j个字符的所有操作集合
  • 属性：操作次数最小值

状态计算

image-20221009142012801 
1
2
3
4
5
6
7
8
9
for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            if(a[i]==b[j]) st[i][j] = st[i-1][j-1];
            else{
                st[i][j] = min(st[i-1][j] + 1,st[i-1][j-1]+1);
                st[i][j] = min(st[i][j],st[i][j-1]+1);

            }
        }

编辑距离

给定n个字符串，以及m次询问，每次询问给出一个字符串和操作上限，求给定的n个字符串中有多少个串可以在操作上限次数内变成询问给出的字符串。

1
2
3
4
5
6
7
8
9
10
11
for(int i=1;i<=n;i++) 
        scanf("%s",strs[i]+1);
for(int i=1;i<=m;i++){
        char tar[K];
        int max_edits;
        scanf("%s%d",tar+1,&max_edits);
        int count = 0;
        for(int j = 1;j<=n;j++)
            if(findMinDis(strs[j],tar)<=max_edits) count++;
        cout<<count<<endl;
}

区间DP

石子合并

n堆石子排成一排，每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，求合并所需的最小代价。

不同的合并顺序需要的体力是不同的

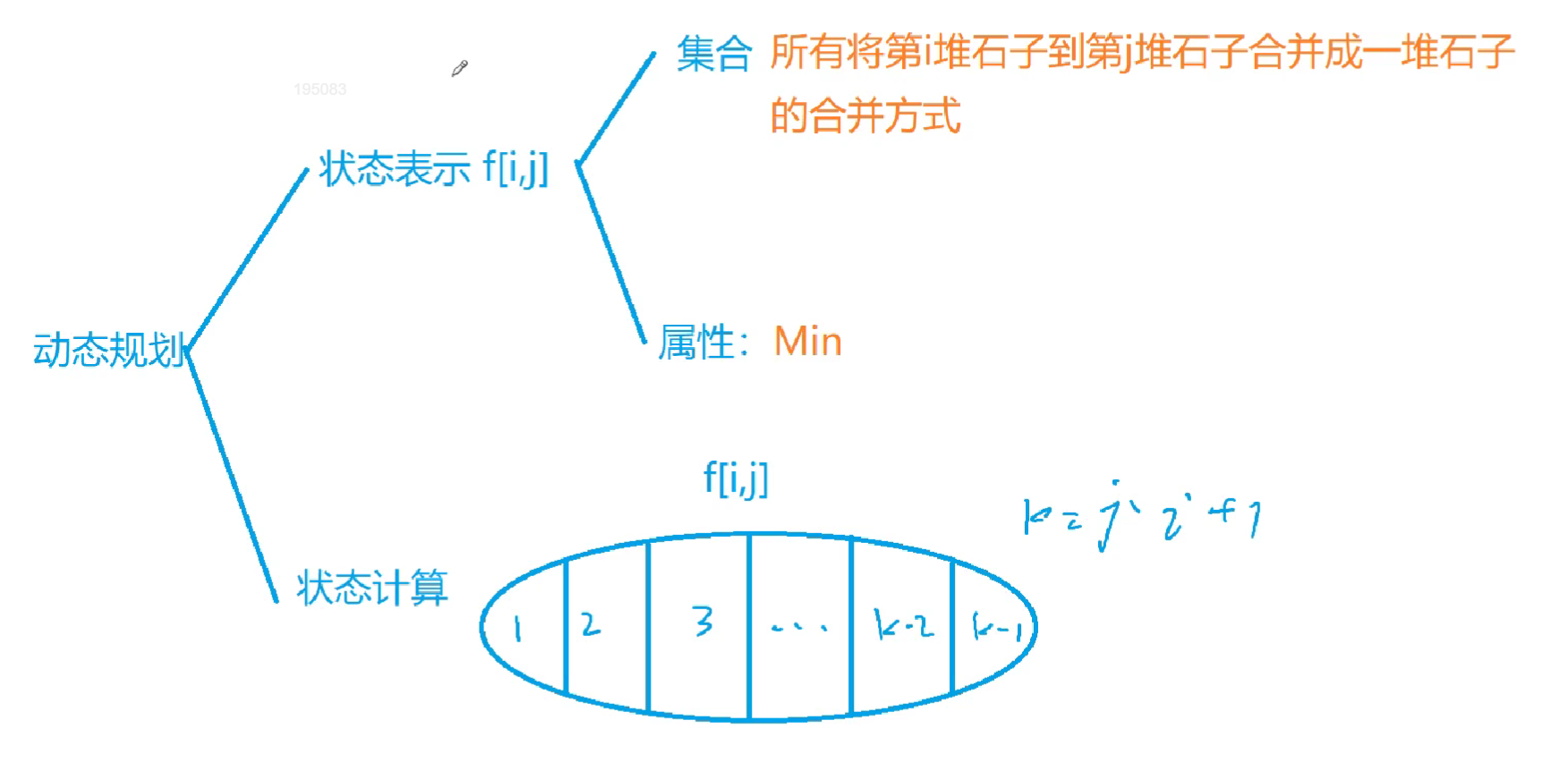
状态表示

  • 集合：从第i堆石子到第j堆石子合并成一堆石子的合并方式
  • 属性：Min

状态计算

image-20220718151622394 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
	for(int i=1;i<=n;i++) cin>>m[i];
    for(int i=1;i<=n;i++) s[i] = s[i-1] + m[i];
    // st[i][j] 表示将第i~j堆石子合并起来的所有方案代价集合的最小代价
    // 要注意状态计算的顺序
    for(int i=1;i<=n;i++) 
        for (int j = i; j <= n; j++) 
            st[i][j] = pinf;
    // 这种遍历方式可以保证区间内的所有可能st均已得到
	// 按区间长度从小到大枚举
    for(int i=n;i>=1;i--)
        for(int j=i;j<=n;j++) {
            if(i==j) st[i][i] = 0;
            for (int k = i; k <= j - 1; k++) {
                st[i][j] = min(st[i][j], st[i][k] + st[k + 1][j] + s[j] - s[i-1]);
//                printf("%d %d : %d ", i,j,st[i][j]);
            }
//            printf("\n");
        }
    cout<<st[1][n]<<endl;

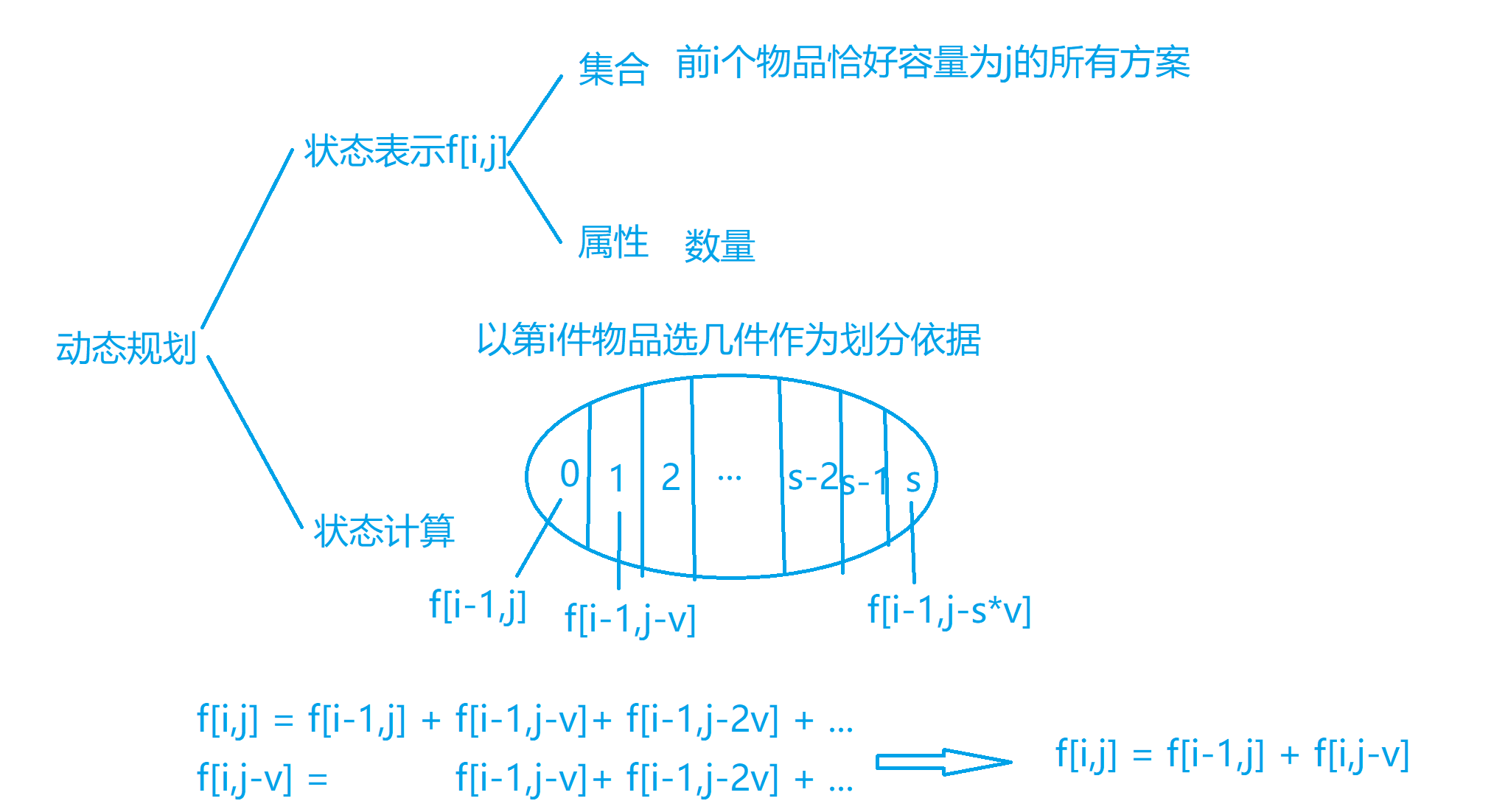
计数类DP

整数划分问题

一个正整数可以表示为若干正整数之和，形如：n=n1+n2+…+nk，其中n1≥n2≥…≥nk，求出n有多少种不同的划分方法。

可以把这个问题作为完全背包问题，背包容量为N，每个物品的体积为1~N，不限个数，问恰好装满背包的方案数。

image-20220725184543921 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 朴素版
	for(int i=0;i<=n;i++) f[i][0] = 1;
    for(int i =1;i<=n;i++)
        for(int j=1;j<=n;j++){
            for(int k=0;k*i<=j;k++){
                f[i][j] = (f[i][j] + f[i-1][j-k*i]) % mod;
            }
        // f[i][j] = f[i-1][j];
        // if(j>=i) f[i][j] = (f[i][j] + f[i][j-i]) % mod;
        }
    cout << f[n][n]<<endl;
// 二维优化版
	for(int i=0;i<=n;i++) f[i][0] = 1;
    for(int i =1;i<=n;i++)
        for(int j=1;j<=n;j++){
            f[i][j] = f[i-1][j];
            if(j>=i) f[i][j] = (f[i][j] + f[i][j-i]) % mod; 
        }
// 一维优化版
fo[0] = 1;
for(int i=1;i<=n;i++)
    for(int j=i;j<=n;j++){
        fo[j] = (fo[j] + fo[j-i]) % mod;
    }

cout << fo[n] << endl;

数位统计DP

计数问题

给定两个整数，求a和b之间所有数字中0~9的出现次数

  • 技巧1：计算a和b之间的所有数字中x的出现次数，可以转换为1b中所有数字中x的次数减去1（a-1）中x的次数
  • 技巧2：计算1n中x的次数，可以通过x在1n中每一位出现的次数求和得到，由题，n可以表示为‘abcdegfh’。

假设我们要求x在第5位出现的次数：

即求出，满足条件1<=abcdxfgh<=n的数有多少个，我们需要分情况进行讨论。

  • 若前4位 mmmm=0000(abcd-1)，无论后三位（nnn=000999）取何值，均满足条件：（abcd * 1000)
  • 若前4位 mmmm=abcd
    • 若第5位e<x : (0)
    • e=x: (nnn=000~fgh, fgh+1)
    • e>x: (nnn=000~999,1000)

特例情况：x=0时需要特殊讨论，即前4位mmmm=1~(abcd-1）并且0不能出现在第一位。其他情况不变

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
using namespace std;
int get_cnt(vector<int> nums, int le,int ri){
    int res = 0;
    for(int i=ri;i>=le;i--){
        res = res * 10 + nums[i];
    }
    return res;
}

int power_10(int num){
    int res = 1;
    for(int i=0;i<num;i++) res *= 10;
    return res;
}

int count_num(int num, int h){
    if(!num) return 0;
    vector<int> nums;
    while(num){
        nums.push_back(num%10);
        num/=10;
    }
    int l = nums.size();
    int res = 0;

    for(int i=0;i<=l-1-!h;i++){
        if(i<l-1) {
            res += get_cnt(nums, i + 1, l - 1) * power_10(i);
            if(!h) res -= power_10(i);
        }
        if(nums[i]>h) res += power_10(i);
        else if(nums[i]==h)
            res += get_cnt(nums,0,i-1)+1;
    }
    return res;
}
void cntNumTest(){
    int a,b;
    while(scanf("%d%d",&a,&b),a||b){
        if(a>b) swap(a,b);
        for(int i=0;i<10;i++)
            printf("%d ",count_num(b,i)-count_num(a-1,i));
        puts("");
    }
}

int main() {
    cntNumTest();
//    mendleanDreamTest();
//    IntDivTest();
    return 0;
}

状态压缩DP

使用整数来表示状态，把这个整数看作是二进制数，每一位是0是1代表不同的情况，因此位数(n)最多取到20位（1e6种状态）

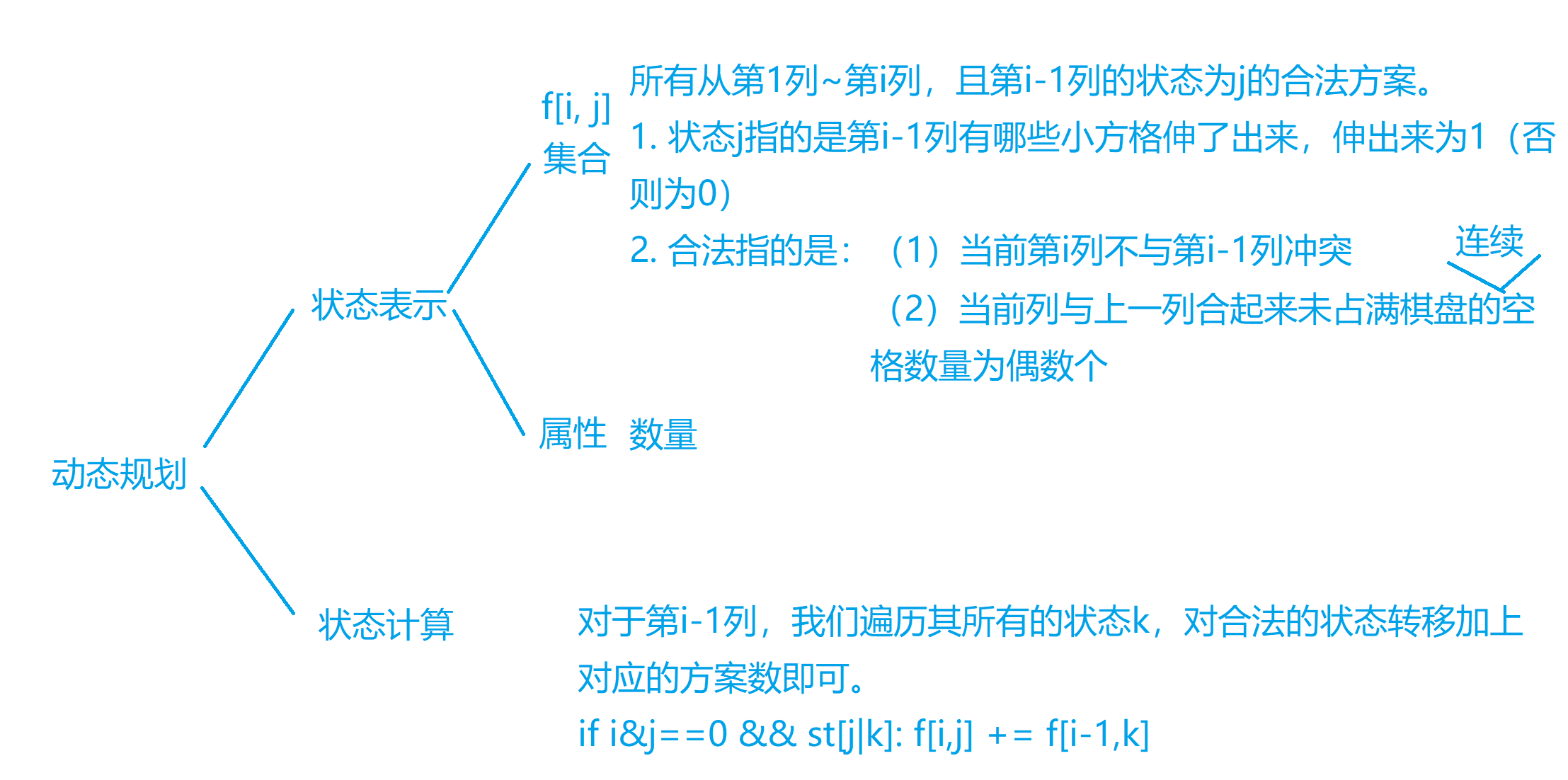
蒙德里安的梦想

求把NM的棋盘分割成若干个12的长方形，有多少种方案。

image-20220728203213749 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <cstring>

using namespace std;
const int M = 13;
bool st[1 << M];
long long fm[M][1 << M];

void mendleanDreamTest() {
    int n, m;
    while (scanf("%d%d", &n, &m), n || m) {
        memset(fm,0,sizeof fm);
        for (int i = 0; i < 1 << n; i++) {
            st[i] = true;
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                if (i >> j & 1) {
                    if (cnt & 1) st[i] = false;
                    cnt = 0;
                } else cnt++;
            }
            if (cnt & 1) st[i] = false;
        }
        fm[0][0] = 1;
        for (int i = 1; i <= m; i++)
            for (int j = 0; j < 1 << n; j++)
                for (int k = 0; k < 1 << n; k++) {
                    if ((j & k) == 0 && st[j | k])
                        fm[i][j] += fm[i - 1][k];
                }
        cout << fm[m][0] << endl;
    }
}
int main() {
//    cntNumTest();
    mendleanDreamTest();
//    IntDivTest();
    return 0;
}

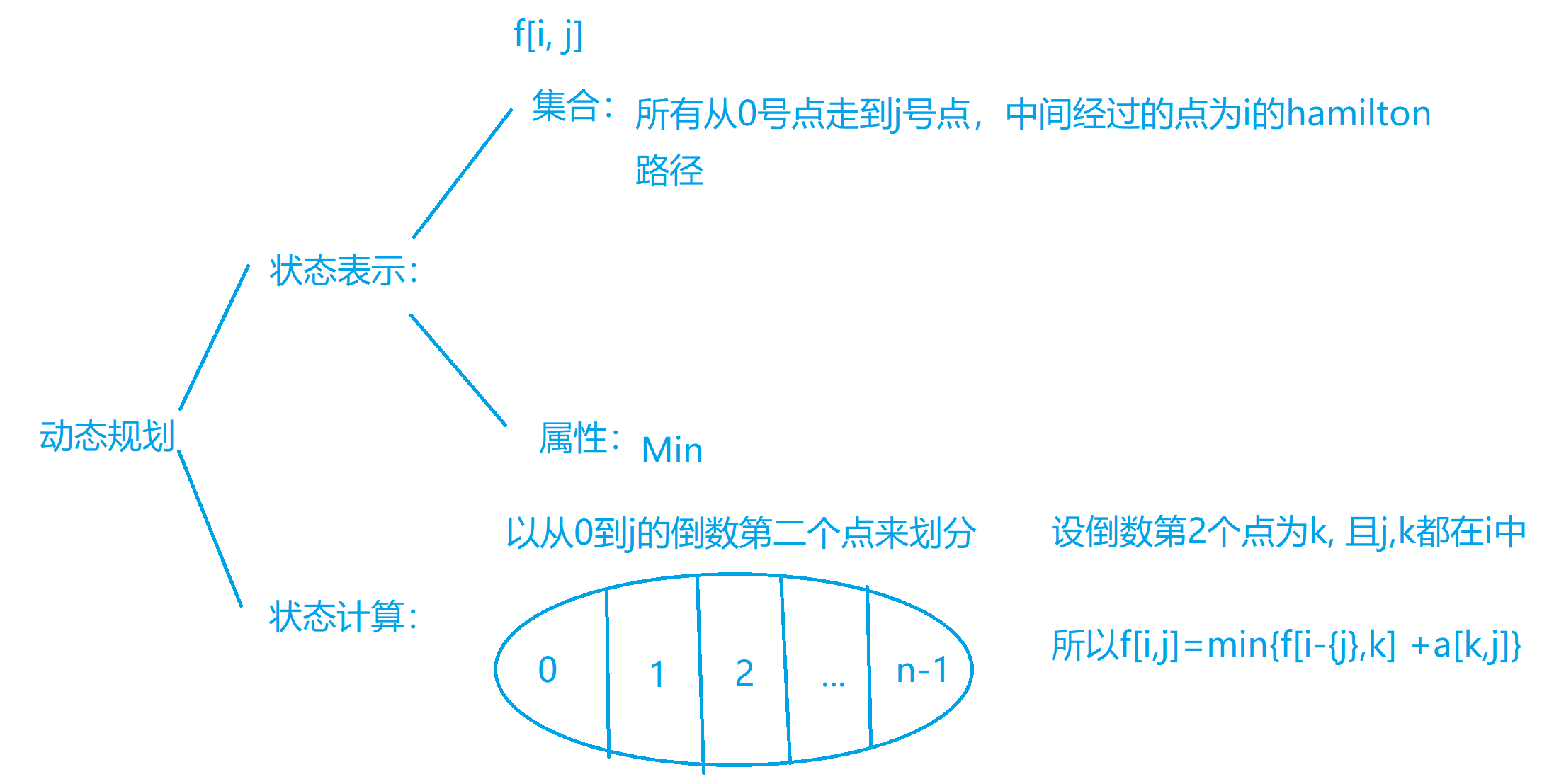
最短Hamilton路径

Hamilton路径：从0到n-1不重不漏地经过每一个点恰好一次

给定n个结点的带权无向图，求起点0到终点n-1的最短Hamilton路径

image-20220729105012006 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstring>
using namespace std;
const int Q = 21;
int a[Q][Q];
int hamil[1<<Q][Q];

void hamiltonTest() {
    int n;
    cin >> n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            scanf("%d", &a[i][j]);
    memset(hamil,0x3f, sizeof hamil);
    hamil[1][0]=0;
    for(int i=0;i<1<<n;i++)
        for(int j=0;j<n;j++){
             if(i>>j&1){
                 for(int k=0;k<n;k++){
                     if(j!=k && i>>k&1){
                         hamil[i][j] = min(hamil[i][j],hamil[i-(1<<j)][k] + a[k][j]);
                     }
                 }
             }
        }
    cout<<hamil[(1<<n)-1][n-1]<<endl;
}

int main() {
    hamiltonTest();
//    cntNumTest();
//    mendleanDreamTest();
//    IntDivTest();
    return 0;
}

树形DP

接受了之后思维跨度就不高

没有上司的舞会

有N名职员，他们的关系为一颗以校长为根的树，父节点就是子结点的直接上司。

每个职员有一个快乐指数，用整数Hi给出，要求邀请一部分职员参会，使得所有的参会职员的快乐指数总和最大，限制是职员不能与其直接上司参会。

思路：因为是树形DP，所以状态可以设置为f[i,j]，在以i为根节点的子树中选择（j=1）或不选择(j=0)根节点的所有选法的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstring>
using namespace std;
const int P= 6010;
int hapi[P];
int h[P],e[P],ne[P],idx;
int mem[P][2];
void insert(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
int proc_node2(int node, int choose){
    if(mem[node][choose]) return mem[node][choose];

    int res = 0;
    if(choose==1){
        res+=hapi[node];
        for(int i = h[node];i!=-1;i=ne[i]) {
            int j = e[i];
            res += proc_node2(j, 0);
        }
    }else{
        for(int i = h[node];i!=-1;i=ne[i]) {
            int j = e[i];
            res += max(proc_node2(j, 0), proc_node2(j, 1));
        }
    }
    mem[node][choose] = res;
    return res;
}
void treeDpTest3(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>hapi[i];
    int root = 1;
    memset(h,-1, sizeof h);
    for(int i=1;i<=n-1;i++){
        int l,k;
        cin>>l>>k;
        insert(k,l);
        if(l==root) root = k;
    }
    int res = max(proc_node2(root,1),proc_node2(root,0));
    cout<<res<<endl;

}
int main() {
    treeDpTest3();

    return 0;
}

记忆化搜索

每一道动规题都可以用递归的方法做

滑雪

给定一个R行C列的矩阵，表示一个矩形网格滑雪场。矩阵中第i行第j列的点表示区域的高度。只有某相邻区域的高度低于自己目前的高度才可滑动到该区域

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<cstring>
#include<iostream>
using namespace std;
const int U = 310;
int board[U][U];
int lens[U][U];
int R,C;
int find_len(int r, int c){
    if(lens[r][c]!=-1) return lens[r][c];
    int di[5]={0,1,0,-1,0};
    for(int i = 0;i<4;i++){
        int x = r + di[i];
        int y = c + di[i+1];
        if(board[x][y]<board[r][c] && x<R && x>=0 && y<C &&y>=0)
            lens[r][c] = max(find_len(x,y) + 1,lens[r][c]);
    }
    if(lens[r][c]==-1) lens[r][c] = 1;
    return lens[r][c];

}
void skiTest(){
    cin>>R>>C;
    for(int i=0;i<R;i++)
        for (int j = 0; j < C; j++)
            scanf("%d",&board[i][j]);
    memset(lens,-1,sizeof lens);
    int res = 0;
    for(int i=0;i<R;i++)
        for (int j = 0; j < C; j++)
            if(lens[i][j]==-1)
                res = max(res,find_len(i,j));
    cout<<res<<endl;

}

int main() {
    skiTest();
    return 0;
}

第七讲 贪心算法

证明困难，没有常用的套路

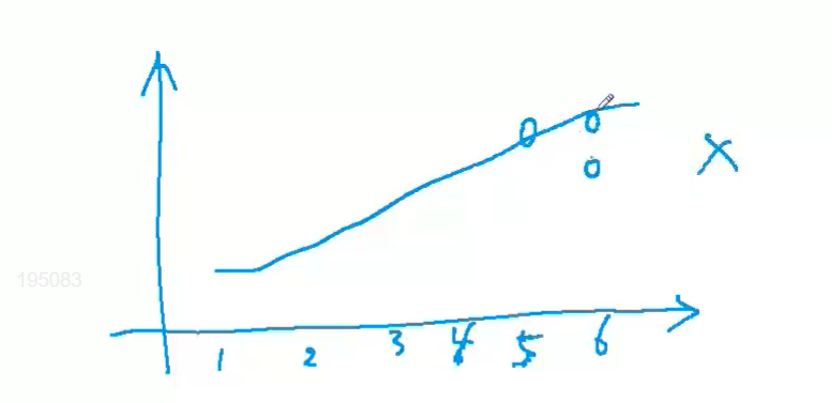
对于区间问题：

  • 左端点排序
  • 右端点排序
  • 双关键字排序
image-20220818121637002

如上图，局部极值不一定是权重最优解，因此只有一个问题是单峰的，才可以用贪心算法来解

区间选点

给定 N个闭区间[ai,bi], 请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。输出选择的点的最小数量。

算法思路

  1. 将每个区间按右端点从小到大排序
  2. 从前往后依次枚举每个区间：
    • 如果当前区间中已经包含选点，则直接pass
    • 否则，选择当前区间的右端点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
struct Range {
    int l, r;

    int operator<(Range &ran) const {
        return r < ran.r;
    }
}ranges[N];

void interSecPntTest() {
    int n;
    cin >> n;
    for(int i=0;i<n;i++){
        int a, b;
        scanf("%d%d", &a, &b);
        ranges[i] = {a,b};
    }
    sort(ranges,ranges+n);
    int ed = -2e9;
    int res = 0;
    for(int i=0;i<n;i++){
        if(ed<ranges[i].l){
            res++;
            ed = ranges[i].r;
        }
    }
    cout<<res<<endl;
}

int main() {
    interSecPntTest();
    return 0;
}

算法证明

  1. Ans <= Cnt

整个算法流程保证了，选出Cnt个点的方案是合法方案，因此有上面的不等式

  1. Ans >= Cnt

选出Cnt个点，实际上是找出了Cnt个不重叠区间，因此选点方案的最小数量至少为Cnt，即Ans>=Cnt

由上，即可证明Ans==Cnt

最大不相交区间的数量

给定N个闭区间[ai,bi]，请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。求可选取区间的最大数量。

算法思路

做法和上一题完全一样

算法证明

Ans是最大不相交区间的数量，Cnt是算法选择的点的数量（Cnt个不重叠区间）

  1. Ans >= Cnt

选出Cnt个点的方案一定是合法方案，所以Ans>=Cnt

  1. Ans <= Cnt

反证法：假设Ans>Cnt，意味着我们可以选出比Cnt更多个互不相交区间；由每一个区间至少包含一个我们选择出来的点，那么根据假设我们至少要选出来Ans个点，这与实际我们最少选出Cnt个点相矛盾，因此Ans <= Cnt

区间分组

给定N个闭区间[ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间没有交集，并使得组数尽可能小。输出最小组数。

算法思路

  1. 将所有区间按左端点从小到大排序
  2. 从前往后处理每个区间
    • 判断能否将其放到某个现有的组中
      • 不能放入(不存在一个组可以放入)，则开新组，然后再将其放进去；
      • 可以放入：L[i] > Max_r，将其放进去，并更新当前Max_r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;
const int N = 1e5+10;
struct Range {
    int l, r;

    int operator<(Range &ran) const {
        return l < ran.l;
    }
}ranges[N];
void interGroupTest(){
    int n;
    cin >> n;
    for(int i=0;i<n;i++){
        int a, b;
        scanf("%d%d", &a, &b);
        ranges[i] = {a,b};
    }
    priority_queue<int, vector<int>,greater<int>> que;
    sort(ranges,ranges+n);
    for(int i=0;i<n;i++){
        if(que.empty() || ranges[i].l <= que.top()){
            que.push(ranges[i].r);
        }
        else{
            que.pop();
            que.push(ranges[i].r);
        }
    }
    cout<<que.size()<<endl;
}
int main() {
//    interSecPntTest();
    interGroupTest();
    return 0;
}

算法证明

Ans是相互补充的的区间的组的最小组数，cnt是算法的组数

  1. Ans <= Cnt

按照算法得到的组数一定是一种合法的方案，而Ans是方案的最小值，因此Ans <= Cnt

  1. Ans >= Cnt

算法开新组的条件是该区间与每个组都有交集，因此Cnt其实是最少开的组的数量（不能更少，否则会有交集），因此Ans >= Cnt

区间覆盖问题

给定N个闭区间[ai,bi]以及一个线段区间[s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。输出最小区间数，如果无法完全覆盖则输出-1。

算法思路

  1. 将所有区间按照左端点从小到大排序
  2. 从前往后依次枚举每个区间，在所有能覆盖开始点的区间中选择右端点最大的区间，若右端点>end，算法退出
    • 若能选出，将start更新成右端点最大值
    • 若找不到满足对应条件的区间，输出-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<algorithm>

using namespace std;
const int N = 1e5 + 10;

struct Range {
    int l, r;

    int operator<(const Range &ran) const {
        return l < ran.l;
    }
} ranges[N];
void interCoverTest() {
    int s, t;
    cin >> s >> t;
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        ranges[i] = {a, b};
    }
    sort(ranges, ranges + n);
    int res = 0;
    for (int i = 0; i < n; i++) {
        
        int max_r = -2e9;
        int j;
        for (j = i; j < n && ranges[j].l <= s; j++) {
            if (ranges[j].r > max_r)
                max_r = ranges[j].r;
        }
        if (max_r == -2e9) {
            cout << "-1" << endl;
            return;
        }
        s = max_r;
        i = j-1;
        res++;
        if(s>=t) break;
    }
    if(s>=t) cout << res << endl;
    else cout<<"-1";
}

int main() {
//    interSecPntTest();
//    interGroupTest();
    interCoverTest();

    return 0;
}

霍夫曼树-合并果子

每一次合并消耗的体力等于两堆果子的重量之和。总耗体力等于每次合并耗的体力之和。设计出合并次序方案，使得消耗的体力最少

算法思路

叶节点到根结点一共有多长，对叶节点就要加多少遍。因此每次挑两个值最小的点相合并，他们深度一定最深，可以互为兄弟。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;
const int M = 10010;
int fruits[M];
void comb_fruitTest(){
    int n;
    cin>>n;
    priority_queue<int,vector<int>,greater<>> que;
    for(int i=0;i<n;i++) {
        scanf("%d",&fruits[i]);
        que.push(fruits[i]);
    }
    int min_cost = 0;
    while(que.size()>1){
        int s1 = que.top();
        que.pop();
        int s2 = que.top();
        que.pop();
        min_cost += s2+s1;
        que.push(s1+s2);
    }
    cout<<min_cost<<endl;

}

int main() {
//    interSecPntTest();
//    interGroupTest();
//    interCoverTest();
    comb_fruitTest();
    return 0;
}

算法证明

  1. 深度最深：假设最小的两个点为a,f，那么b,f交换后一定收益为正
image-20220818145334644

  1. 可以互为兄弟：a,b,c,d顺序可以交换，不影响全局最优解

  2. 合并剩下n-1个果子的最优解一定是合并n个果子的最优解吗？

    即f(n) = f(n-1)+a+b成立吗？

    因为合并果子一定可以先合并最小两个点作为最优解，所以对于所有方案都可以把（a+b）去掉不影响最值，因此原问题就可以变为n-1个点的huffman问题，所以合并剩下n-1个果子的最优解一定是合并n个果子的最优解

排序不等式

可能会爆int，所以用Long Long来做

算法思路

按照从小到大的顺序排队，总时间最小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<iostream>
#include<algorithm>

using namespace std;
const int N = 100010;
int q[N];
typedef long long LL;
void MinWaitTimeTest(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++) scanf("%d",&q[i]);
    sort(q,q+n);
    LL res = 0;
    for(int i=0;i<n-1;i++){
        res += q[i]*(n-i-1);
    }
    cout<<res<<endl;
}
int main(){
    MinWaitTimeTest();
    return 0;
}

算法证明

调整法

若不是排好序的，那么一定存在ti>ti+1,若我们将ti和ti+1交换位置，那么交换前比交换后多了ti-ti+1>0，也就是说交换完后总时间就会降低。

绝对值不等式

算法思路

按照从小到大排序，取中位数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<algorithm>

using namespace std;
const int N = 100010;
int q[N];

void MinDistTest(){
    int n;
    cin>>n;
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    sort(q,q+n);
    int res =0;
    for(int i=0;i<n;i++){
        res += abs(q[n/2]-q[i]);
    }
    cout<<res<<endl;

}

int main() {
//    MinWaitTimeTest();
    MinDistTest();
    return 0;
}

算法证明

分组法

只要x位于a,b之间，就可以取到最小值。分组后对每一个组都可以取到最小值，同时取即是总共的最小值，即取到正中间即可。

推公式

基于不等式来证明贪心问题

耍杂技的牛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<algorithm>

using namespace std;
const int C = 50010;
typedef pair<int, int> pii;
pii ent[C];

void MinRiskTest() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int w, s;
        scanf("%d%d", &w, &s);
        ent[i] = {w + s, s};
    }
    sort(ent, ent + n);
    int res = -2e9;
    int sum = 0;
    for (int i = 0; i < n; i++) {
        int s = ent[i].second;
        int w = ent[i].first - s;
        res = max(res, sum - s);
        sum += w;
    }
    cout<<res<<endl;
}

int main() {
//    MinWaitTimeTest();
//    MinDistTest();
    MinRiskTest();
    return 0;
}

算法思路

按照wi+si从小到大的顺序排，最大的危险系数一定是最小的

算法证明

只要最优解不是严格从小到大递增的，我们一定可以找到第i个位置上的牛和第i+1位置上的牛他们满足，交换完这两个牛后，我们可以证明，这两个危险系数的最大值一定会严格变小

  • Post title：coding笔记：Acwing知识点总结
  • Post author：sixwalter
  • Create time：2023-08-05 11:14:26
  • Post link：https://coelien.github.io/2023/08/05/coding-solution/acwing总结/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.
 Comments