acwing 1296 聪明的燕姿

Description

城市中人们总是拿着号码牌，不停寻找，不断匹配，可是谁也不知道自己等的那个人是谁。

可是燕姿不一样，燕姿知道自己等的人是谁，因为燕姿数学学得好！

燕姿发现了一个神奇的算法：假设自己的号码牌上写着数字 S，那么自己等的人手上的号码牌数字的所有正约数之和必定等于 S。

所以燕姿总是拿着号码牌在地铁和人海找数字（喂！这样真的靠谱吗）。

可是她忙着唱《遇见》，想拜托你写一个程序能够快速地找到所有自己等的人。

Input

输入包含 k组数据。

对于每组数据，输入包含一个号码牌 S。

Output

对于每组数据，输出有两行。

第一行包含一个整数 m，表示有 m 个等的人。

第二行包含相应的 m个数，表示所有等的人的号码牌。

注意：你输出的号码牌必须按照升序排列。

Solution

求所有公约数之和

每个约数均不相同，且是选法数量之一。

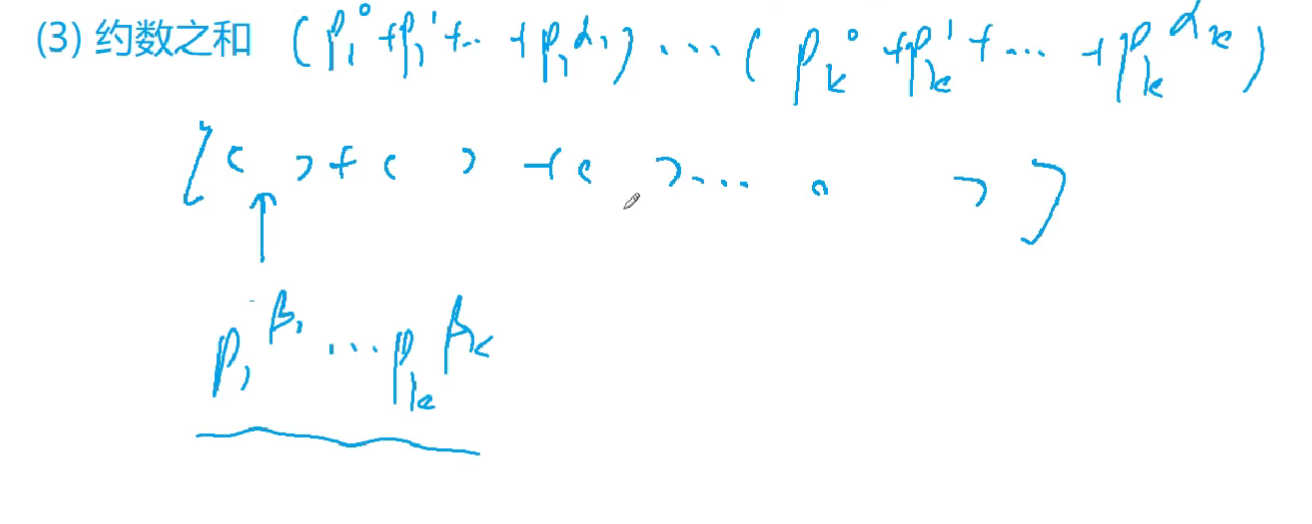
$S = (p_1^0+p_1^1+…+p_1^{a1})(p_2^0+p_2^1+…+p_2^{a2})…*(p_k^0+p_k^1+…+p_k^{ak})$

for(int j = 1+pri, t = pri; j<=x; t*=pri, j+=t){
            if(x%j==0){
                // printf("%d %d %d %d %d\n",x, pri, a, pri_a, sum_pr);
                dfs(x/j,i+1,tmp * t);
            }
}

上面的代码可以同时求出总和和每一项的值（等差数列求和）
避免使用pow函数(溢出风险+复杂度高)
终止条件: j>x

一种优化的判定质数的方法

初始版

bool is_prime(int n){
    if(n<N) return !st[n];
    for(int i=0;primes[i]<=n/primes[i];i++)
        if(n%primes[i]==0) return false;
    return true;
}

利用已知信息+

bool is_prime(int n){
    if(n<N) return !st[n];
    for(int i=2;i<=n/i;++i)
        if(n%i==0)
            return false;
    return true;
}

只使用质数来判定

bool is_prime(int n){
    if(n<N) return !st[n];
    for(int i=0;primes[i]<=n/primes[i];i++)
        if(n%primes[i]==0) return false;
    return true;
}

只有第三种才能AC，但感觉需要防止越界（i<cnt），但不加也可以AC
后两种方法都需要先预处理出质数
核心思想：我们可以发现n的所有约数都是成对出现的，即若d为n的约束，那么n/d也为n的约数。所以我们不需要枚举所有数，只需要枚举的质数即可，也就是说d只需枚举到即可

dfs遍历顺序

依次枚举p，a
p(2,3,5,7,…)
a(1,2,3,) // 在代码中未显示地枚举，而是用乘积代替，本质上是一个意思
if(S mod j == 0)
- dfs(…)

优化（剪枝）

如果，且pi比之前的质因子大的话（需要满足等式条件）直接可以将pi作为结果的因子
如果，我们只需要遍历小于的质因子即可（因为）

code

#include<iostream>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;

const int N = 50010;
int primes[N];
int cnt = 0;
bool st[N];
int res[N], len;

void getPrimes(int n){
    primes[1] = true;
    for(int i=2;i<=n;++i){
        if(!st[i]) primes[cnt++] = i;
        for(int j=0; primes[j]*i<=n;++j){
            st[primes[j]*i] = true;
            if(i%primes[j] == 0) break;
        }
    }
}

bool is_prime(int n){
    if(n<N) return !st[n];
    for(int i=0;primes[i]<=n/primes[i];i++)
        if(n%primes[i]==0) return false;
    return true;
}

void dfs(int x, int idx, int tmp){
    if(x == 1) {
        res[len++] = tmp;
        return;
    }
    if(x-1>(idx==0?1:primes[idx-1]) && is_prime(x-1)){
        res[len++] = tmp*(x-1);
    }
    for(int i = idx;i<cnt;++i){ 
        int pri = primes[i];
        if(pri >= sqrt(x))
            break;
        for(int j = 1+pri, t = pri; j<=x; t*=pri, j+=t){
            if(x%j==0){
                dfs(x/j,i+1,tmp * t);
            }
        }
    }
    

}
int main(){
    getPrimes(N-1);
    int x;
    while(cin>>x){
        len = 0;
        dfs(x,0,1);
        printf("%ld\n",len);
        sort(res,res+len);
        for(int i=0;i<len;++i){
            printf("%d ",res[i]);
        }
        if(len) printf("\n");
    }
}