二分算法

整数二分

整数二分因为涉及+1，-1，所以为了防止死循环，需要考虑边界情况。
当我们定义一个性质，该性质可以将数据二分时（即存在边界时），二分算法是可以将该边界找出来的。

主要思想

假设在整个区间内部是可以找到答案的，我们对整个区间不断进行二分
每次都要选择答案所在的区间去进行下一步搜索（每次会把整个区间的大小缩小一半）
二分一定会保证区间里有答案的，但是存在特例，即原问题无解的情况（无解一定和题目有关）
在原问题无解的情况下，若没有遇到数组边界，找到的区间一定是满足条件的，但不是query；而如果遇到数组边界，那么就可能不会满足找到的区间一定是满足条件的（以整数的范围这道题为例）

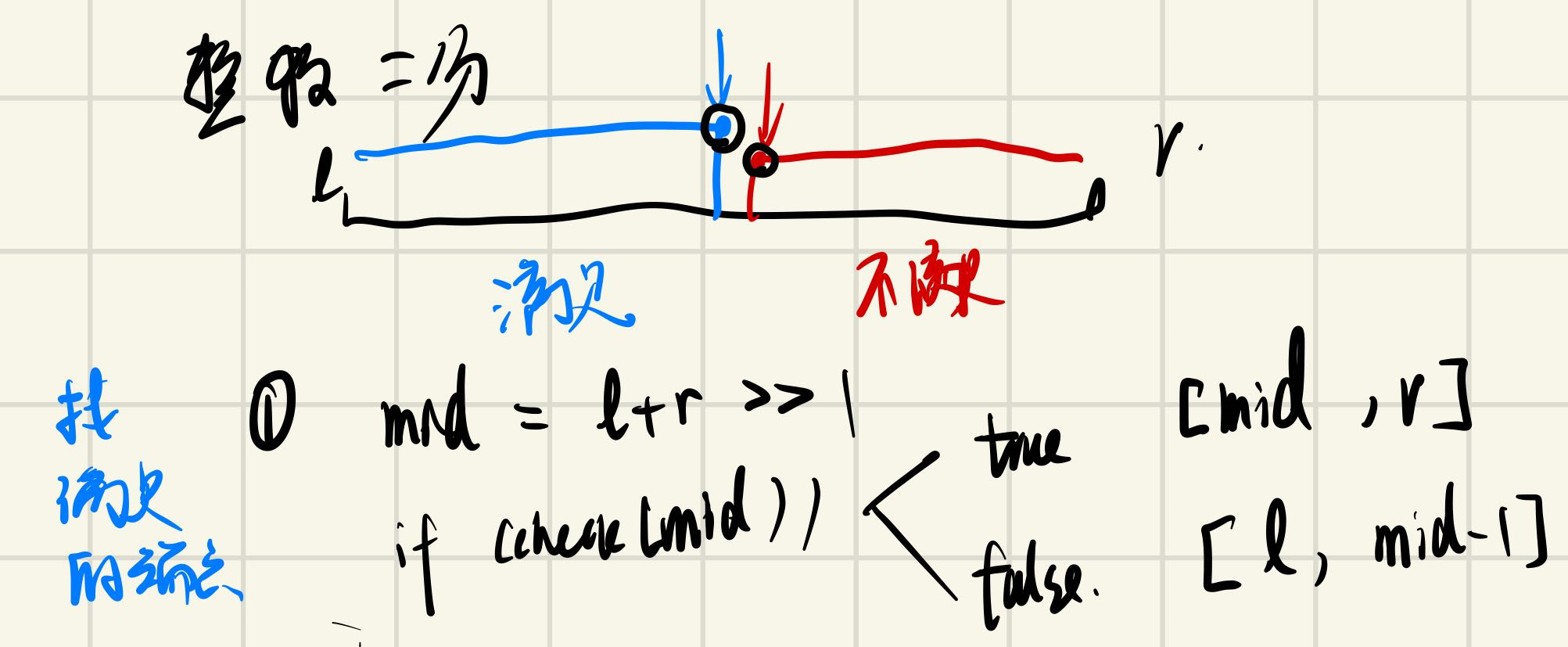
该图即为寻找满足check的最右端端点示意图

上图对应的代码即为二分模板1的代码，如下所示：

bool check(int mid) {return false;}
double function(double){return 0.0;}
// 二分模板1
int bsearch1(int l,int r){
    // 考虑边界，l+1=r时，算法是否正确
    // l+1=r时,需要修改mid=l,会陷入死循环
    // 所以修改mid=(l+r+1)/2,遇到边界时，mid=r,可以顺利退出
    // r会小于l的可能仅在最后一句，但遇到边界且不满足条件时，计算的mid不可能=l,所以退出循环时r不可能小于l,即l=r
    // 返回r,l均可
    while (l<r){
        int mid = l+r+1 >>1;
        // 若check 代表满足条件
        if(check(mid)) l = mid;
        else r = mid-1;
    }
    return l;
}
// 二分模板2
int bsearch2(int l,int r){
    // 寻找不满足的断点
    // 考虑边界，l+1=r时，算法是正确的
    // 退出循环时，l==r的原理同上
    while(l<r){
        int mid = l+r>>1;
        if(check(mid)) l = mid+1;
        else r = mid;
    }
    return l;
}

浮点数二分

较整数二分简单，因为不需要考虑边界（因为没有整除，每次都可以完美地将边界缩小一半）
思想与整数二分一样，只要满足时时刻刻答案都在我们的区间即可；
但我们的区间足够小时，我们就可以认为已经找到了答案；
有两种方式可以去写浮点数二分的循环条件：一个是固定循环100次，如果原来区间长度为1时，结束时区间长度即为；或是指定一个很小的数epsilon，当区间长度小于这个数即可退出。

double fbsearch(double l,double r,double target){
    // 浮点数二分查找
    while(r-l>1e-8){
        double mid = (l+r)/2;
        double val = function(mid);
        if (val>=target) r = mid;
        else l = mid;
    }
    return l;
}

应用：数的三次方根

求数的三次方根可以使用二分查找来做。因为函数是单调的，所以很容易判断mid和target的大小关系，从而缩小查找范围，代码如下：

double fbiSearch(double l, double r, double target, double (*pf)(double)) {
    while (r - l > 1e-7) {
        double mid = (l + r) / 2;
        if (pf(mid) <= target) l = mid;
        else r = mid;
    }
    return r;
}
double calTrip(double x){
    return x*x*x;
}
int findRoot3(){
    double n;
    double (*pf)(double)=calTrip;
    cin>>n;
    if(n<0) printf("-%.6f",fbiSearch(0,ceil(-n),-n,calTrip));
    else printf("%.6f",fbiSearch(0,ceil(n),n,calTrip));
    return 0;
}

简要介绍下引入的函数指针，有了函数指针就可以方便地将计算方法传入二分查找算法来找解。double (*pf)(double)=calTrip;可以定义一个函数指针，非常有用。