问题空间搜索

DFS

执着的算法

思想

会尽可能往深了搜，搜不到了就回溯，每一次回溯完之后判断当前是不是所有的路径均已遍历，若均已遍历，再进行回溯，否则搜索未遍历的路径
两个重要概念
- 回溯
  
  注意恢复现场
- 剪枝
  
  最优性剪枝：当前的路径判断一定不如最优解，就可以剪枝了
  
  可行性剪枝：提前判断当前方案一定是不合法的，那么下面的子树就可以不用进行搜索了
顺序：重要的是顺序，即我们要用一个什么样的顺序将某一道题的所有方案全部遍历一遍
举例：

全排列问题—最经典DFS的问题

const int N = 10;
int path[N];
bool st[N];
//求1-n的全排列数量
void dfs(int h,int n){
    if(h==n){
        for(int i=0;i<n;i++)
            printf("%d ",path[i]);
        puts("");
    }
    for(int i=1;i<=n;i++){
        if(!st[i]){
            path[h] = i;
            st[i] = true;
            dfs(i,h+1,n);
            st[i] = false;
        }
    }
}

n-皇后问题

第一种搜索顺序：枚举每一行这个皇后应该放到哪一列上去（经过了某种程度的优化，因为两个皇后不可能在同一行），与全排列的搜索顺序完全一致，同一对角线上的元素必定满足上图的直线方程，所以可以用截距b作为直线的编号。

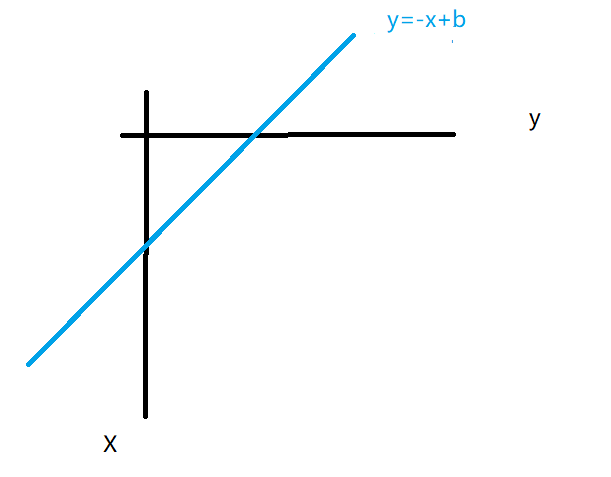
const int N = 20;
bool col[N];
bool diag[2*N],udiag[2*N];
char Q[N][N];
// 无需对queencnt计数，比视频里的方法快了4，5ms
void initBoard(int n){
    for(int i = 1;i<=n;i++) {
        for (int j = 1; j <=n; j++)
            Q[i][j] = '.';
    }
}
void nqueen_dfs(int r,int n){
    for(int i=1;i<=n;i++){
        if(!col[i]&&!diag[i+r]&&!udiag[i-r+n]){
            
            col[i] = diag[i+r]= udiag[i-r+n] = true;
            Q[r][i] = 'Q';
            
            if(r==n){
                for(int k=1;k<=n;k++){
                    for(int j=1;j<=n;j++){
                        printf("%c",Q[k][j]);
                    }
                    puts("");
                }
                puts("");
                Q[r][i] = '.';
                col[i] = diag[i+r]= udiag[i-r+n] = false;
                return;
            }
            
            nqueen_dfs(r+1,n);
            Q[r][i] = '.';
            col[i] = diag[i+r]= udiag[i-r+n] = false;
        }
    }
}

第二种搜索顺序：更加原始的一种搜索方式，对于每一个格子，选择是否放皇后，挨个枚举所有格子，当枚举到最后一个格子(N^2)的时候即得到答案

对于这种思路我们应该如何处理呢？

BFS

稳重的算法

思想

每次扩展一层，只有当前层全搜索过了之后，才会去搜索下一层，第一次搜到的话一定是最短的

DFS和BFS对比

搜索方式	数据结构	占用空间	最短路性质	应用场景
DFS	stack	O(h)	不可以搜到最短路	对空间要求高的
BFS	queue	O(2^h)	可以搜到最短路（边权重为1时）	最小步数，最短距离，最少操作次数

举例：

走迷宫—最短路问题；dp问题实际上是没有环的最短路

基本框架
- 将初始状态放入队列
- 只有队列不空便循环:
  - 每次把队头拿出来
  - 扩展队头

//迷宫问题--如何将框架应用起来

//数据准备与初始化
int g[N][N]; // store the map
int d[N][N]; // store the distance to the start entry

int bfs()