快排的应用

第k个数

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k个数。

输入格式

第一行包含两个整数 n 和 k

第二行包含 n 个整数（所有整数均在 1∼10^9 范围内），表示整数数列。

输出格式

输出一个整数，表示数列的第 k 小数。

数据范围

1≤n≤100000
1≤k≤n

输入样例

1 2	5 3 2 4 1 5 3

输出样例

主要思想

如果先排序再取第k个数，会导致的复杂度，因此采用快速选择算法，基于快排的模板进行修改即可：

int findKthNumber(int q[],int l,int r,int k){
    if(l==r) return q[l];
    int mid = l+r>>1;
    int x = q[mid];
    int i = l-1,j = r+1;
    while(i<j){
        do{i++;}while(q[i]<x);
        do{j--;}while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    int lol = j-l+1;
    if(k<=lol) return findKthNumber(q,l,j,k);
    else return findKthNumber(q,j+1,r,k-lol);
}

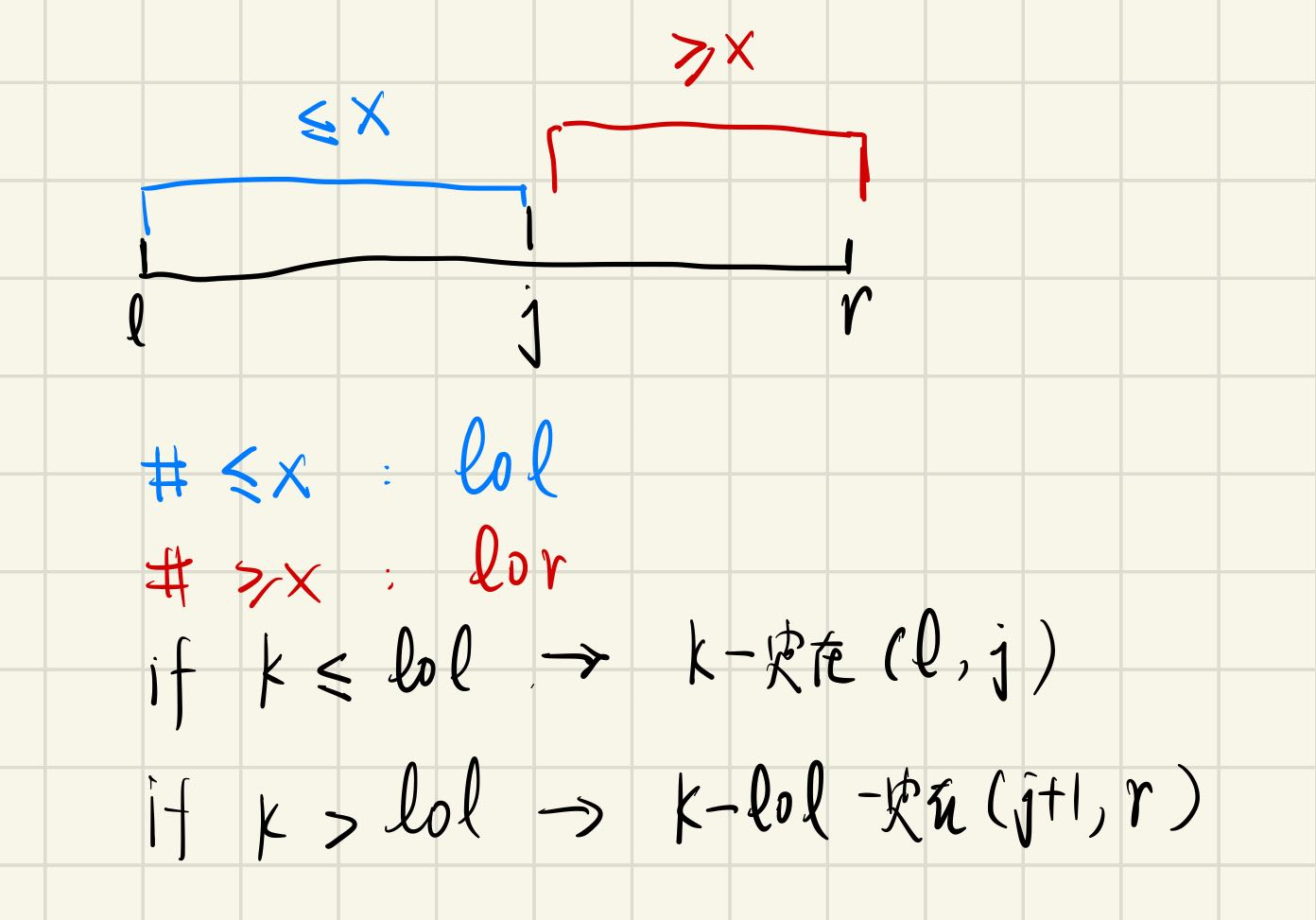
如上图所示，修改点在于如何递归地处理子问题：在（l,r）中寻找第k个数。
而快排给出了找到良好分界点的方式，即j左边的数包括j自身都小于等于x，j右边的数都大于等于x。
因此蓝色区间的数都小于等于红色区间的数，从而如果k小于等于蓝色区间的数的个数，那么第k个数一定在蓝色区间中；反之，如果k大于蓝色区间的数的个数，那么第k个数一定大于等于x,即在红色区间中可以找到。

疑惑与解释

最难理解的地方其实在于边界处，如果k==lol，即第k个数刚好是蓝色区间的个数，我们是否可以直接返回x呢？答案是否定的。原因在于j这个点其实决定了蓝色区间的长度，但是这不代表x就处于j这个位置，即[l..j]可能都小于x，因此第k个数不一定就是x，下图是一个实例，直观解释了这一点：

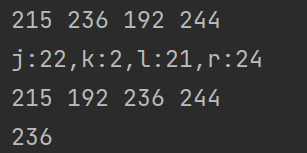
上图中x是236，j=22指向192这个数，lol=2=k，可见215，192都小于x(236)，236，244都大于等于x，但是返回的却不是第k个数。k=lol只能说明下一步要去寻找蓝色区间里最大的数。