KMP算法浅析

KMP算法在各种参考书中均有讲解，但均较为复杂，且不易于理解其中原理，现佐以笔记，记录自己的学习心得

因为kmp算法相对抽象，因此本文大多辅以图像方便理解

参考视频：https://www.bilibili.com/video/BV1MY4y1Y7Nh

问题描述

给定一个模式串 S，以及一个模板串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串 P 在模式串 S 中多次作为子串出现。

求出模板串 P 在模式串 S 中所有出现的位置的起始下标。

输入格式

第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式

共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围

1≤N≤105
1≤M≤106

核心思想

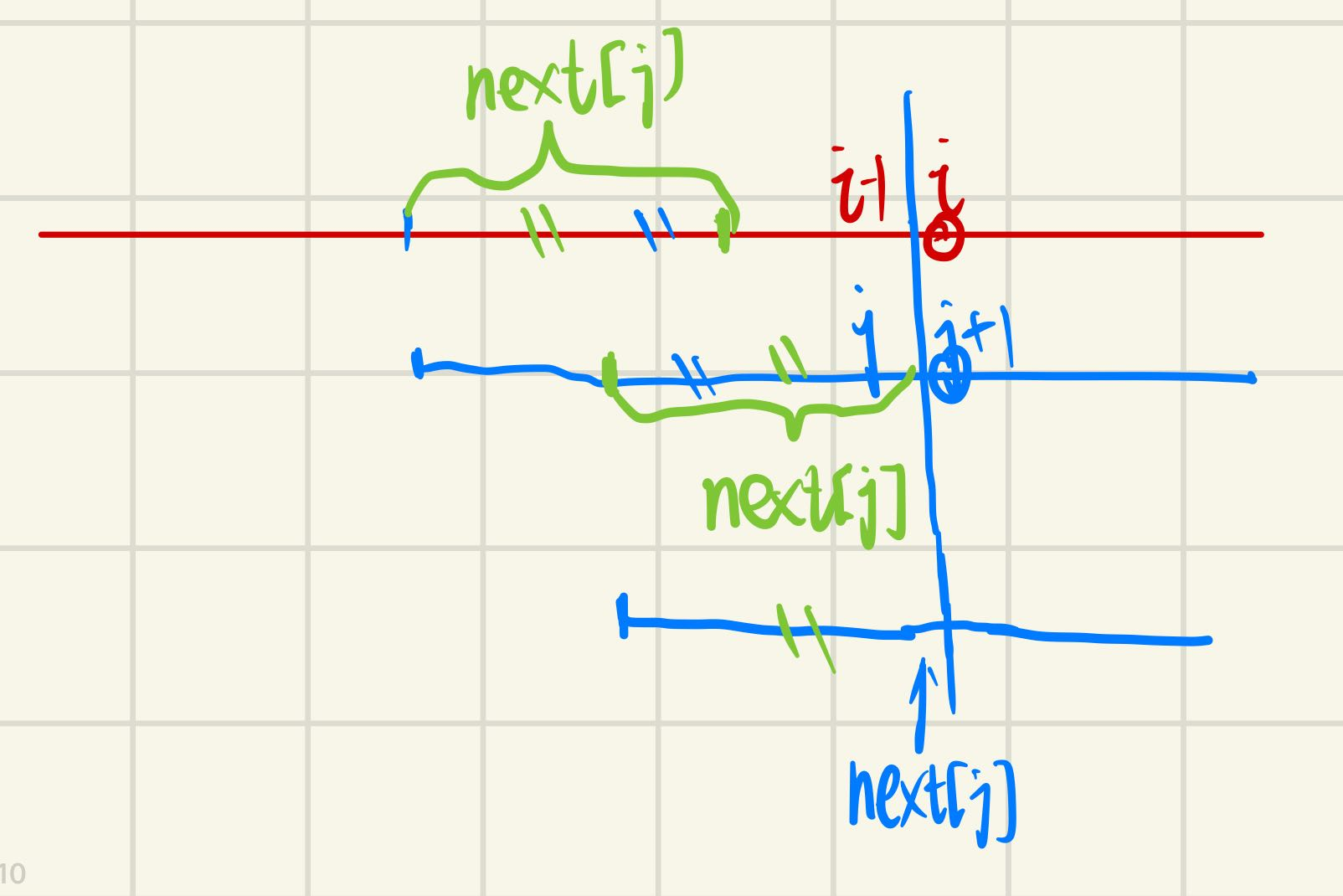
如图，假设现在已匹配了j个字符，但是第j+1个字符不匹配，即，这里S为红色的目标串，P为蓝色的模式串。不匹配时，需将模式传尽可能少的往后移动（我的理解是为了防止漏掉正解），使得移动后的模式串仍与目标串匹配且长度为next[j]，这里采用的思想是不浪费过去已匹配的信息的同时确保找到所有的解，这里只需简单的令即可减少无用的重复匹配次数，然后再判断P[next[j]+1]和S[i]是否相等，不相等则重复上述步骤直到j=0。

最大前后缀相等长度

上述的next[j]的定义为：P[1,j]的前缀和后缀相等的最大长度，之所有取最大前文也有解释，是为了确保找到所有解。

next数组求解

既然问题的关键在于求解next数组，那么找到行之有效的算法是很必要的。这里的思想为归纳法：假设我们已经求解出了next[1,i-1]，现在求出next[i]即可归纳求出整个next数组。依旧可以看上面的图，因为next[i-1]已知，我们可以把模式串移到对应的位置，判断P[i]是否等于P[next[i-1]+1]。若相等说明next[i] = next[i-1] + 1；若不等令P[next[next[i-1]]+1]和P[i]再进行判断，若一直不满足，那么直到next[…] = 0，说明P[1,i]的前缀和后缀相等的最大长度为0，因此next[i]则为0。

next[i] = next[i-1] + 1

下面用反证法解释下为什么该式是成立的：若存在一个更长的前缀和后缀相等的子串，那么同时去掉一个刚匹配的字符，则剩下的串比next[i-1]也要长，这与假设next[i-1]已经是最长的相互矛盾，因此next[i]所存的就是P[1,i]的前缀和后缀相等的最大长度。

// 求解next数组
for(int i=1,j=0;i<=n;i++){
    while(j && P[j+1]==P[i]) j = ne[j];
    if(P[j+1]==P[i]) j++;
    ne[i] = j;
}

// kmp匹配
for(int i=1,j=0;i<=m;i++){
    while(j && P[j+1]==S[i]) j = ne[j];
    if(P[j+1]==S[i]) j++;
    if(j==n){
        print("%d ", i-n);
        j = ne[j];
    }
}

KMP算法应用

字符串的循环节

next数组的解法可以让我们求出字符串的循环节：n-next[n]

由图，因为绿色字符串的前缀和后缀相等的最大长度为next[n]，因此我们可以将该串向后移动n-next[n]，使得重叠部分恰好相等。又因为下面的串是平移的，因此上面串的第一段就等于下面串的第一段且长度为n-next[n]，又下面串的第一段与上面串的重叠部分相等（第二段），因此上面串的第一段和第二段相等，以此类推上面串的所有段都相等且以n-next[n]为长度进行循环，因此是字符串的循环节。

不具有循环节的串

例如，“abcdefgh”,不重复的串是不可能有循环节的，若是以其作为模式串，next[i]均为0，kmp算法最多比较O(m+n)次

循环节最多的串

例如，“aaaaaaa”，每个字符都相等的串的循环次数最多，若是以其为模式串，kmp算法最多比较匹配O(2m)次

详细证明可参考博客

字符串所有前后缀相等的子串

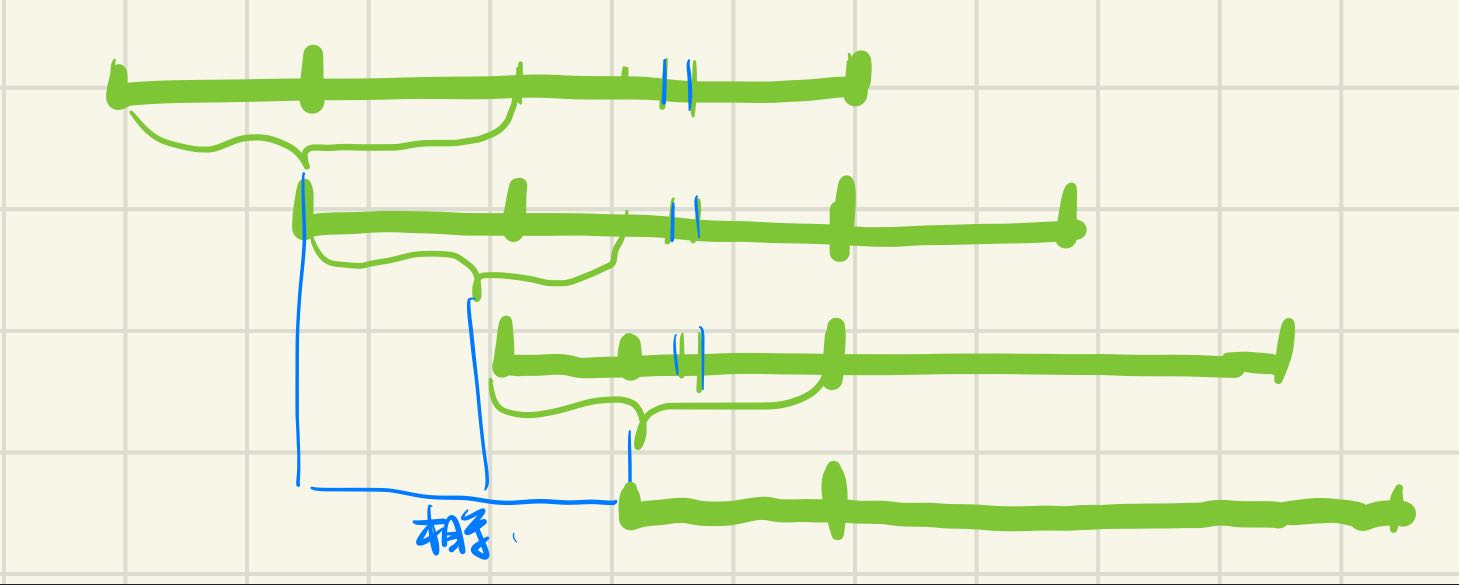
这个求解实际和循环节的求解是完全相似的。每次我们将字符串向后平移(实际上是令j = next[j])，求出next数组后我们可以很方便的求出其所有前缀与后缀相等的子串P[:next[j]], j = next[j] util j = 0

现证明该算法为什么能找到所有前后缀相等的子串

假设存在长度为k的前后缀未能通过上述递归式找到。我们先去找长度大于k的长度为i_t的前后缀，假设找到了且为图中第一段的next[n]，那么下一段next[next[n]]即是以next[n]为结尾的最长的前后缀，因为k也是前后缀，但是k比next[next[n]]长与next[next[n]]的定义相互矛盾，所以k必然不存在，因此算法找到了所有前后缀相等的子串。