如何准备蓝桥杯？

如何准备？

1. 过知识点（10个重要的），从历年题中抓10个最频繁出现的point
2. 例题的思路搞懂，再做一遍
3. 做习题题目

重点

• 刷题量
• 调试

套路

一般ACM或者笔试题的时间限制是1秒或2秒。

在这种情况下，C++代码中的操作次数控制在 为最佳。

下面给出在不同数据范围下，代码的时间复杂度和算法该如何选择：

1. , 指数级别, dfs+剪枝，状态压缩dp
2. ，floyd，dp，高斯消元n
3. ，dp，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford
4. ，块状链表、分块、莫队
5. => 各种sort，线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
6. , 以及常数较小的 算法 => 单调队列、 hash、双指针扫描、并查集，kmp、AC自动机，常数比较小的的做法：sort、树状数组、heap、dijkstra、spfa
7. ，双指针扫描、kmp、AC自动机、线性筛素数
8. ，判断质数
9. ，最大公约数，快速幂，数位DP
10. ，高精度加减乘除
11. ，k表示位数，高精度加减、FFT/NTT

递归

斐波那契数列

1.2.3.5.8.13

递推式：

int fibo(int n){
    if(n==1) return 1;
    if(n==2) return 2;
    return fibo(n-1)+fibo(n-2);
}

如何思考递归问题？

所有递归都可以转化为一颗递归搜索树，例如对斐波那契数列而言：

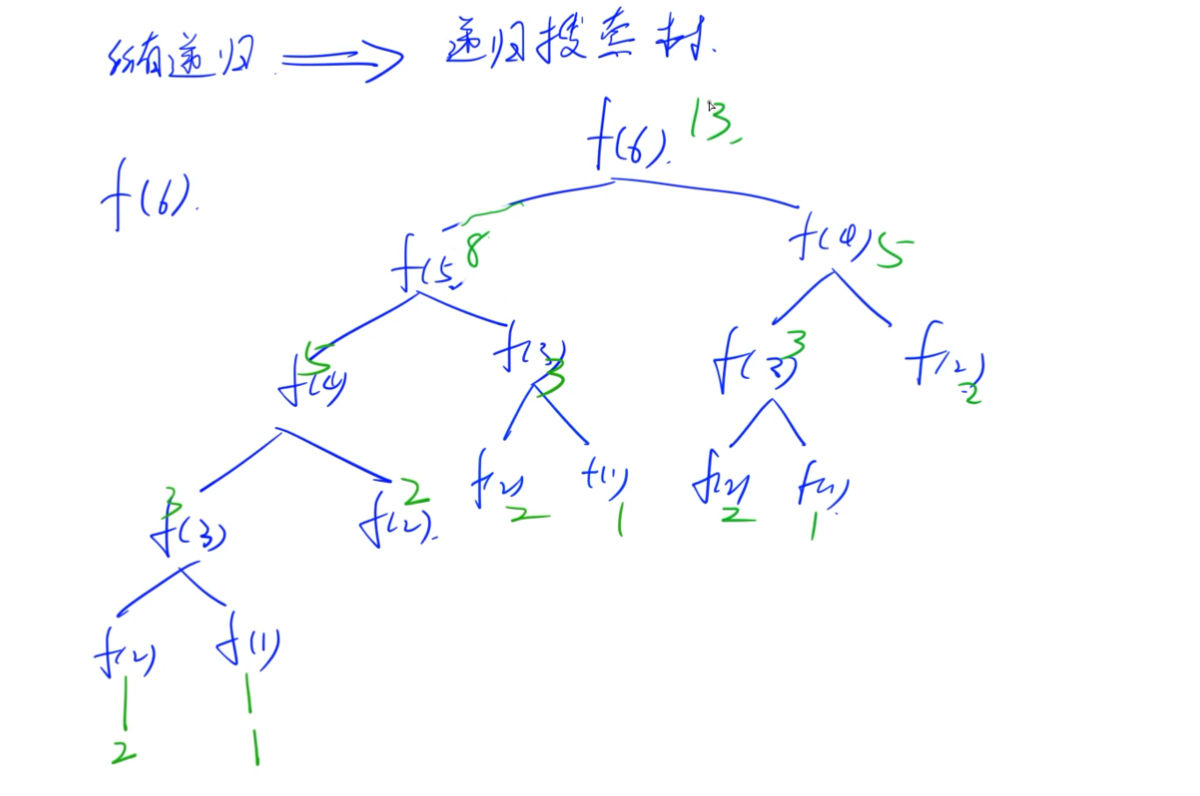
递推

当前步的操作（状态）由上步的状态推出

费解的开关

25 盏灯排成一个 5×5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

给定一些游戏的初始状态，编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。

思想

首先，枚举第一行的所有可能操作（1：改变状态，0：不改变状态），当一行的所有操作确定之后，只有第二行才能改变第一行的状态。因此此时如果第一行的某个灯目前是暗的，第二行对应的灯必须要进行操作来使第一行的灯变亮。以此类推，前四行所有灯都变亮后（实际上每行的灯都进行了操作，所以不能再操作了），如果最后一行还有暗的就是无解。

怎么存数据

• 用int二维数组

  int sq[N][N];
  char in_str[N];
  //要做一个转换，多了一步
  for (int i = 0; i < 5; i++) {
              cin >> in_str;
              for (int j = 0; in_str[j]; j++) {
                  sq[i][j] = in_str[j] - '0';
              }
  }

• 用char二维数组

  char sq[N][N];
  // 无需转换
  for (int i = 0; i < 5; i++)
      cin>>sq[i];
  // 但在转变状态时需要注意
  sq[i][j] = sq[i][j]^1;

飞行员兄弟

这是一道和上题极像的题，但思路总体来说是枚举而非递推。首先同一个位置不能操作两次，对于每一个位置，有两种选择，要么操作，要么不操作。因此可以使用01串来表示操作的状态。对于4*4的网格，一共有2^16种可能的操作方案。暴力枚举，找最少操作数的方案即可。

int board[4][4];
int temp_board[4][4];
char temp_str[5];
typedef pair<int,int> pii;
vector<pii> pairs,res;
void solu_116(){
    for(int i=0;i<4;i++){
        cin>>temp_str;
        for(int j=0;j<4;j++){
            if(temp_str[j]=='-') board[i][j]=1;
        }
    }
    int min_step = 17;
    for(int i=0;i<1<<16;i++) {
        int step = 0;
        pairs.clear();
        memcpy(temp_board,board, sizeof board);
        for (int j = 0; j < 16; j++) {
            if (i >> j & 1) {
                oper(j / 4, j % 4);
                pairs.push_back({j / 4, j % 4});
                step++;
            }
        }
        bool can_sol = true;
        for (int p = 0; p < 4; p++)
            for (int q = 0; q < 4; q++)
                if (!temp_board[p][q]) {
                    can_sol = false;
                    break;
                }
        if (can_sol) {
            if (step < min_step) {
                min_step = step;
                res.clear();
                for (auto elem: pairs)
                    res.push_back(elem);
            }
        }
    }
    cout<<min_step<<endl;
    for (auto elem: res)
        printf("%d %d\n", elem.first+1, elem.second+1);

}

二分

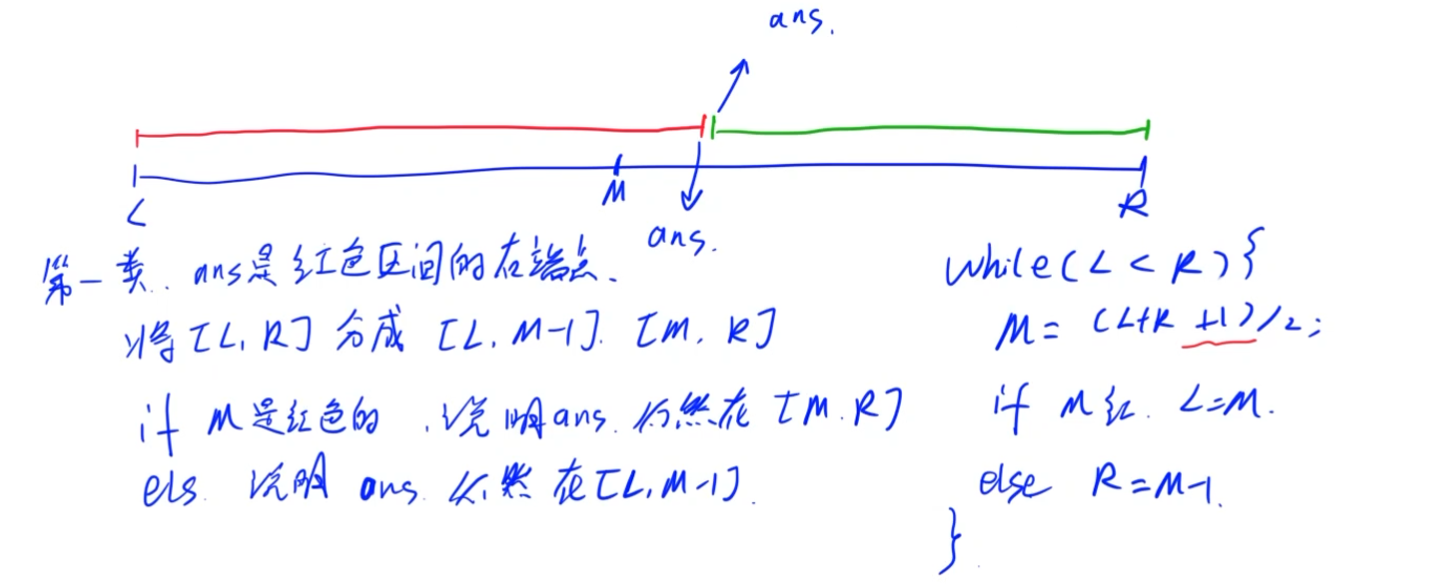
• 确定一个区间（L，R），使得目标值一定在区间中
• 找一个性质（判断条件），满足两点：
  • 性质具有二段性
  • 答案是二段性的分界点
• 分析中点M在该判断条件下是否成立，若成立，考虑答案在哪个区间；如果不成立，考虑答案在哪个区间。