论文阅读笔记：“Aggregated Residual Transformations for Deep Neural Networks”

我想读一些关于网络架构设计的文章，也许会有利于我搭建自己的network，虽然说他们只是2D的架构但是迁移到3D应该不是很困难

核心亮点

lego blocks

ResNeXt继承了VGG的思想，就是使用一种简单但是有效的策略来构建深度网络：像堆乐高积木一样，使用大小相同的building block来构建，这个block可以是多个层的组合，多个block具有相似的拓扑结构。这种思路不仅有利于代码实现，也可以减少需要调整的超参数。他还有一个“致命”的好处就是减少超参数对于特定数据集的过度适应。

split-transform-merge

“分离，变换，合并”，听起来很抽象，但实际上很易懂。一个最简单的neuron可以帮助我们更好地理解这个思想：

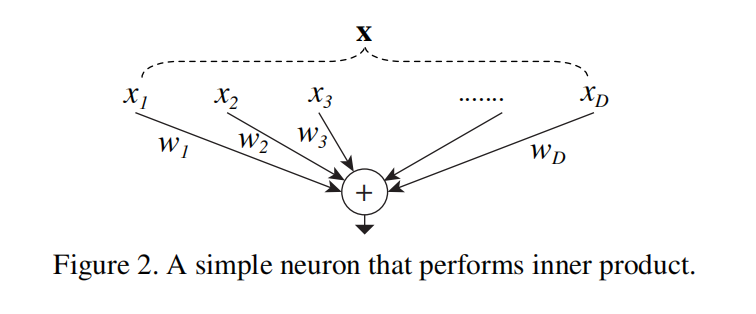
对于一个向量x，我们对其使用神经元来处理，实际上就是将x在其特征维度分解为一个个标量（split），对于每一个变量乘以对应的权重（transform），最后将这些值进行求和（merge）。

更加形式化地，可以将split-transform-merge表示为：

可以为任意地函数，它会将x投影到低维度的embedding，再对其进行transform，C代表cardinality，也就是分组的组数。

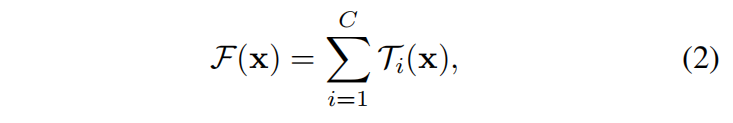
group convolutioon

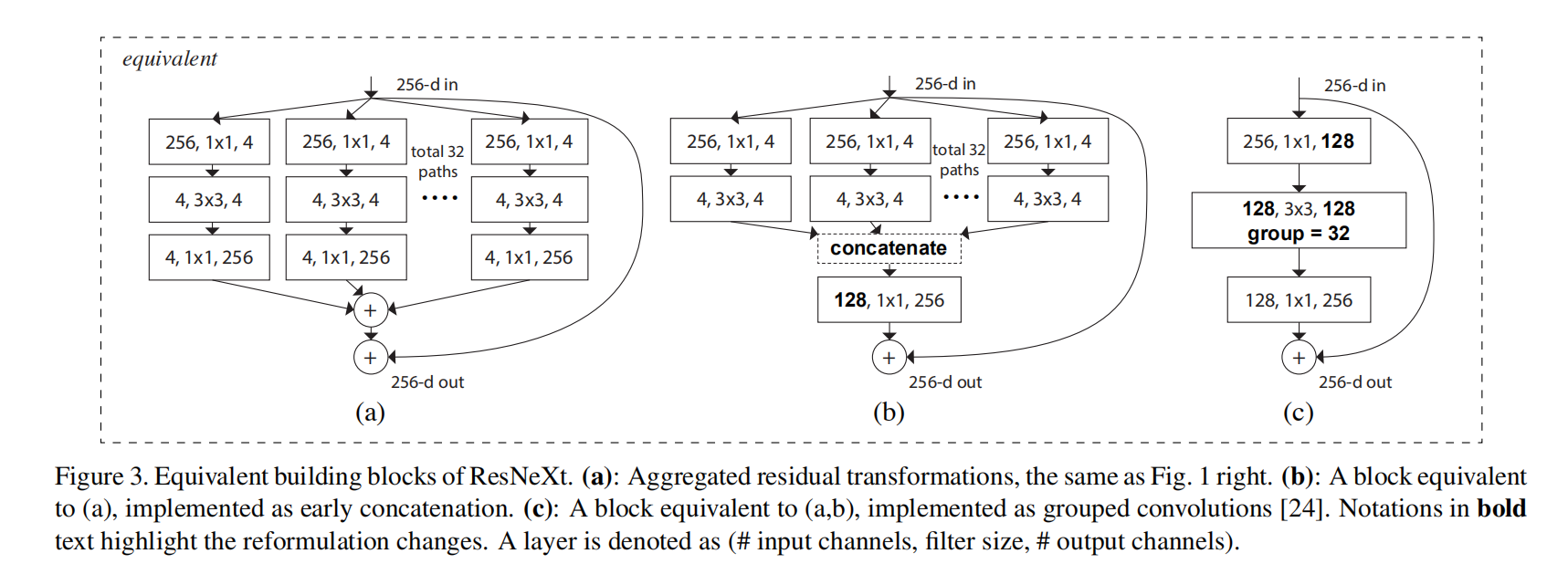
分组卷积是上述两个思想的自然延深和实际应用，因为每个block的拓扑结构均相同，因此通道的数量也可以作为参数来进行实验。如图c中，分组卷积实际上就是执行了32组的输入和输出channel均为4的卷积。

亮点思考

为什么分组卷积可以降低复杂度？

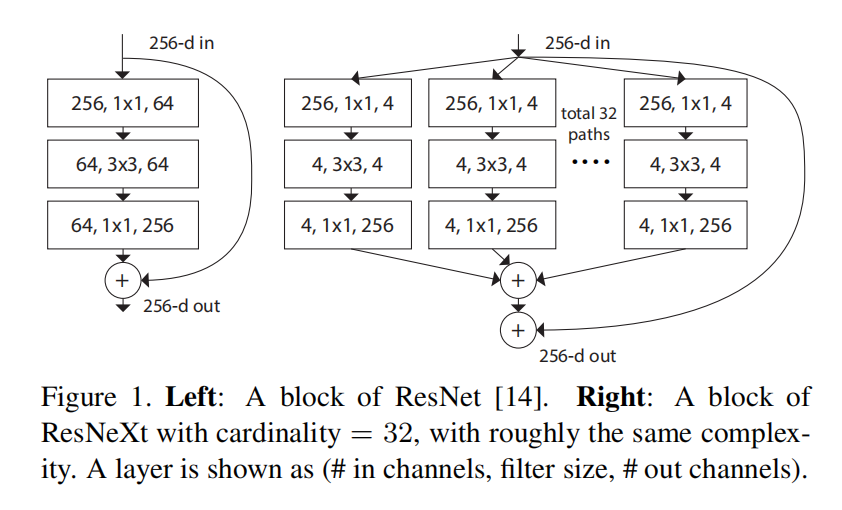
从上图可以看出，左边block的复杂度近似等于右边的block，右边block也与图3的(c)block等价，因此感觉处理的通道数明明变多了，但实际上复杂度却近似相同。

从计算的角度设输入的大小为（t,t)，那么左边block的运算量为：

$tt25664+tt*(33642)64+tt64256=106496t^2$

右边block的计算量为：

$(tt2564+tt*(3342)4+tt4256)32 + tt25631=82688t^2$

为了计算方便我省去了padding，因其对计算量影响不大。从计算可见右边block的计算量实际比左边要小（文中说的等价实际上是参数数量的等价，这个更好计算，这里不再赘述），这也证明了使用分组卷积可以大大降低计算量。

从直观上进行理解的话是，虽然bottleneck更加wider，但是连接更加稀疏，因此需要计算和训练的参数也更少。

channel-wise conv && group conv

channer-wise conv实际上分组卷积的特例，它将通道维度进行了split，令cardinality等于输入通道数

模型架构

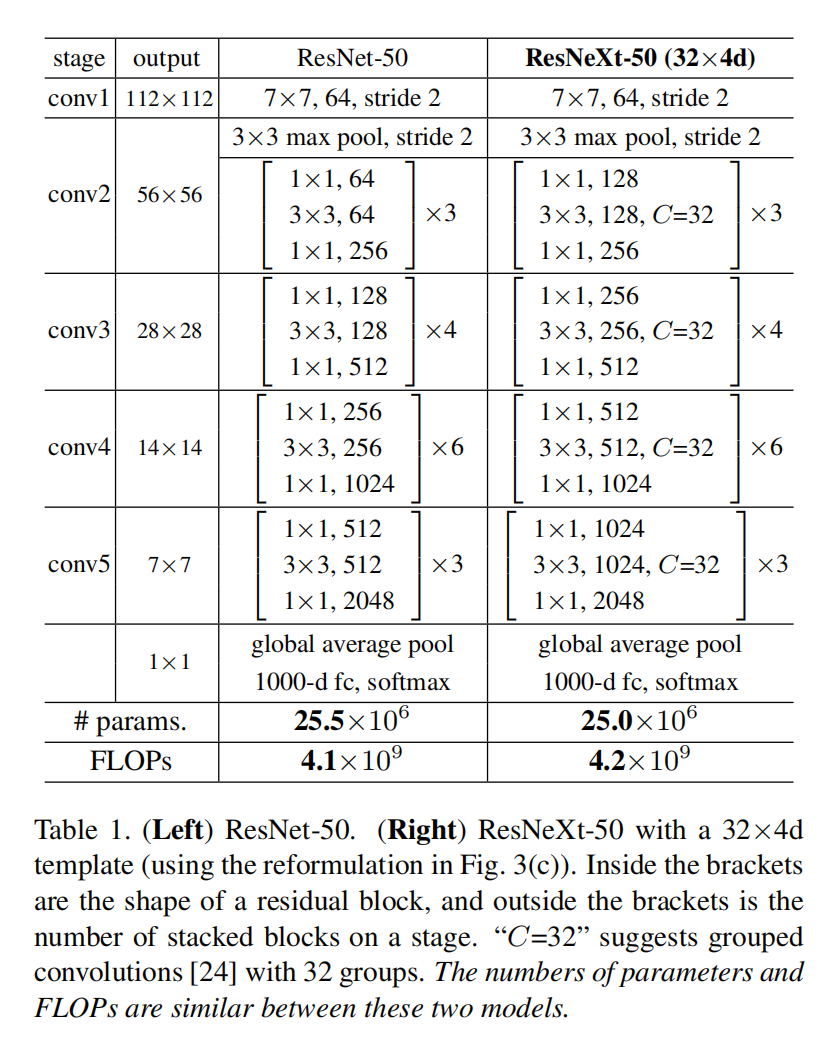
关键结论

新维度 cardinality

基数（split的组数），可以作为设计深度架构的一个新的维度，必要时可以将其纳入考虑。